Zadanie nr 7818635
Trapez, w którym jedna z podstaw jest dwa razy dłuższa od drugiej, podzielono odcinkiem łączącym środki ramion trapezu na dwa czworokąty. Oblicz stosunek pól otrzymanych czworokątów.
Rozwiązanie
Rozpoczynamy od rysunku
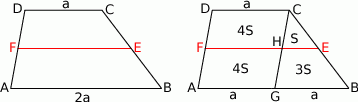
Sposób I
Jak wiadomo odcinek łączący środki ramion trapezu jest równoległy do podstaw (twierdzenie odwrotne do twierdzenia Talesa) i ma długość równą średniej arytmetycznej długości podstaw trapezu. W wyniku podziału otrzymaliśmy więc dwa trapezy oraz
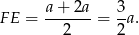
W takim razie stosunek pól trapezów jest równy
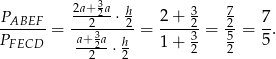
Sposób II
Jeżeli nie pamiętamy wzoru na długość odcinka łączącego środki ramion trapezu, możemy sobie poradzić następująco. Poprowadźmy odcinek 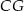 równoległy do ramienia
równoległy do ramienia 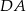 . W ten sposób podzieliliśmy wyjściowy trapez na dwa równoległoboki, trapez i trójkąt. Oznaczmy pole trójkąta przez
. W ten sposób podzieliliśmy wyjściowy trapez na dwa równoległoboki, trapez i trójkąt. Oznaczmy pole trójkąta przez 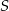 . Trójkąt
. Trójkąt 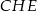 jest podobny do trójkąta
jest podobny do trójkąta 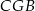 w skali 1:2 więc jego pole stanowi
w skali 1:2 więc jego pole stanowi 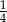 pola trójkąta
pola trójkąta 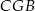 . Zatem pole trapezu
. Zatem pole trapezu 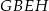 musi być równe
musi być równe 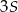 . Teraz zauważmy, że trójkąt
. Teraz zauważmy, że trójkąt 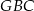 i równoległobok
i równoległobok 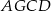 mają równe podstawy i wysokości, więc pole
mają równe podstawy i wysokości, więc pole 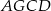 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 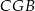 , czyli jest równe
, czyli jest równe 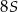 . To oznacza, że pola równoległoboków
. To oznacza, że pola równoległoboków 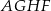 i
i 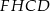 są równe
są równe 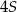 i szukany stosunek pól jest równy
i szukany stosunek pól jest równy
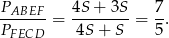
Odpowiedź: 

