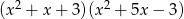Zadanie nr 7521255
Przedstaw wielomian 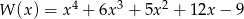 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i tak, aby współczynniki przy drugich potęgach były równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i tak, aby współczynniki przy drugich potęgach były równe jeden.
Rozwiązanie
Sposób I
Szukamy rozkładu postaci
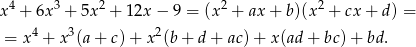
Dwa wielomiany są równe jeżeli mają równe współczynnik przy odpowiadających potęgach  . Otrzymujemy zatem układ równań
. Otrzymujemy zatem układ równań
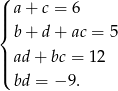
Rozwiązywanie tego układu równań byłoby bardzo nieprzyjemne, ale na szczęście wiemy, że liczby 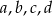 mają być liczbami całkowitymi. Ostatnie równanie daje nam 6 możliwości:
mają być liczbami całkowitymi. Ostatnie równanie daje nam 6 możliwości:
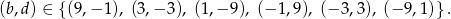
Aby zmniejszyć liczbę możliwości, zauważmy, że ze względu na symetryczną rolę poszukiwanych wielomianów 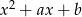 i
i 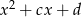 , możemy założyć, że
, możemy założyć, że 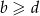 . Przy takim założeniu pozostają nam trzy pary.
. Przy takim założeniu pozostają nam trzy pary.
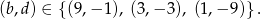
Sprawdzamy teraz każdą z par, podstawiając do pozostałych równań układu.
Jeżeli 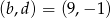 to mamy układ równań
to mamy układ równań
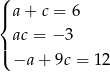
Jeżeli dodamy pierwsze i trzecie równanie stronami, to otrzymamy 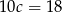 , co jest niemożliwe (bo
, co jest niemożliwe (bo  ma być liczbą całkowitą).
ma być liczbą całkowitą).
Jeżeli 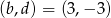 to mamy układ równań
to mamy układ równań
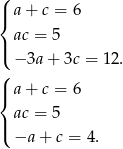
Dodając pierwsze i trzecie równanie otrzymujemy 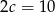 , czyli
, czyli 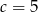 . Wtedy
. Wtedy 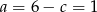 . Widać, że liczby te spełniają też drugie równanie. Otrzymujemy więc w tym przypadku rozwiązanie
. Widać, że liczby te spełniają też drugie równanie. Otrzymujemy więc w tym przypadku rozwiązanie 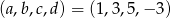 .
.
Jeżeli wreszcie 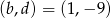 to mamy układ równań
to mamy układ równań
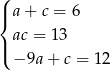
Jeżeli odejmiemy od pierwszego równania trzecie to otrzymamy 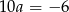 , co jest niemożliwe (bo
, co jest niemożliwe (bo  ma być liczbą całkowitą).
ma być liczbą całkowitą).
Zatem jedyny możliwy rozkład to
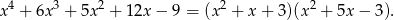
Sposób II
Jeżeli ktoś jest spostrzegawczy, to może zauważyć, że dany wielomian jest różnicą dwóch kwadratów.
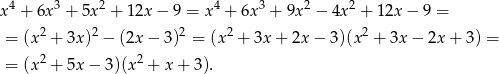
Odpowiedź: