/Szkoła średnia/Zadania maturalne/Matura 2018/Matura
Egzamin Maturalny
z Matematyki poziom rozszerzony 9 maja 2018 Czas pracy: 180 minut
Zadania zamknięte
Dane są liczby 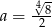 ,
, 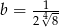 ,
, 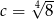 ,
, 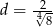 oraz
oraz 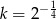 . Prawdziwa jest równość
. Prawdziwa jest równość
A) 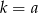 B)
B) 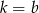 C)
C) 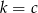 D)
D) 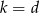
Równanie 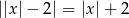
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie cztery rozwiązania.
Wartość wyrażenia 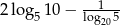 jest równa
jest równa
A) 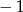 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Granica 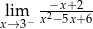 jest równa
jest równa
A) 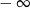 B)
B) 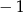 C) 0 D)
C) 0 D) 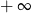
Zadania otwarte
Punkt 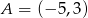 jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem
jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem  , gdy
, gdy 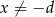 . Oblicz iloraz
. Oblicz iloraz  .
.
Styczna do paraboli o równaniu 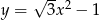 w punkcie
w punkcie 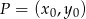 jest nachylona do osi
jest nachylona do osi 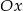 pod kątem
pod kątem 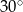 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 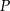 .
.
Trójkąt 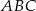 jest ostrokątny oraz
jest ostrokątny oraz 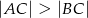 . Dwusieczna
. Dwusieczna 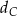 kąta
kąta 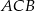 przecina bok
przecina bok 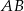 w punkcie
w punkcie 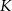 . Punkt
. Punkt 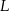 jest obrazem punktu
jest obrazem punktu 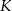 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 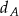 kąta
kąta 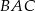 , punkt
, punkt 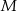 jest obrazem punktu
jest obrazem punktu 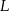 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 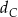 kąta
kąta 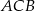 , a punkt
, a punkt 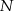 jest obrazem punktu
jest obrazem punktu 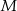 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 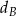 kąta
kąta 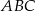 (zobacz rysunek).
(zobacz rysunek).
Udowodnij, że na czworokącie 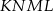 można opisać okrąg.
można opisać okrąg.
Udowodnij, że dla każdej liczby całkowitej 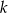 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 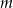 liczba
liczba 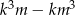 jest podzielna przez 6.
jest podzielna przez 6.
Z liczb ośmioelementowego zbioru 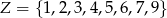 tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
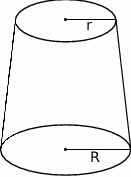
Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru 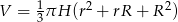 , gdzie
, gdzie  i
i 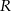 są promieniami podstaw (
są promieniami podstaw (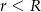 ), a
), a 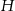 jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość
jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość 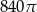 , a
, a 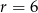 . Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
. Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.
Rozwiąż równanie 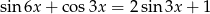 w przedziale
w przedziale 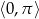 .
.
Wyznacz wszystkie wartości parametru 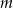 , dla których równanie
, dla których równanie 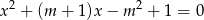 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 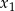 i
i 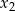
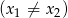 , spełniające warunek
, spełniające warunek 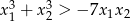 .
.
Wyrazy ciągu geometrycznego 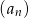 , określonego dla
, określonego dla 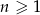 , spełniają układ równań
, spełniają układ równań
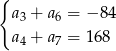
Wyznacz liczbę  początkowych wyrazów tego ciągu, których suma
początkowych wyrazów tego ciągu, których suma 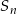 jest równa 32769.
jest równa 32769.
Punkt 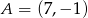 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 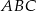 , w którym
, w którym 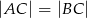 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 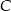 są liczbami ujemnymi. Okrąg wpisany w trójkąt
są liczbami ujemnymi. Okrąg wpisany w trójkąt 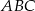 ma równanie
ma równanie 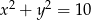 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 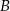 i
i 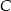 tego trójkąta.
tego trójkąta.
Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, spełniające warunek: suma długości dłuższej podstawy  i wysokości trapezu jest równa 2.
i wysokości trapezu jest równa 2.
- Wyznacz wszystkie wartości
 , dla których istnieje trapez o podanych własnościach.
, dla których istnieje trapez o podanych własnościach. - Wykaż, że obwód
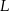 takiego trapezu, jako funkcja długości
takiego trapezu, jako funkcja długości  dłuższej podstawy trapezu, wyraża się wzorem
dłuższej podstawy trapezu, wyraża się wzorem 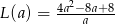
- Oblicz tangens kąta ostrego tego spośród rozpatrywanych trapezów, którego obwód jest najmniejszy.

