/Szkoła średnia/Zadania maturalne/Matura 2019
Lubelska próba przed maturą
z matematyki poziom podstawowy grupa I 5 marca 2019 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem nierówności 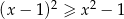 jest zbiór
jest zbiór
A) 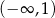 B)
B) 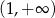 C)
C) 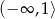 D)
D) 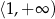
Wyrażenie 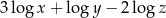 jest równe
jest równe
A) 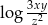 B)
B) 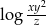 C)
C) 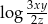 D)
D) 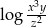
Liczba o 10% mniejsza od liczby, która jest o 20% większa od liczby 1200 jest równa
A) 1340 B) 1296 C) 1440 D) 1080
Suma liczby odwrotnej do 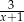 i przeciwnej do
i przeciwnej do 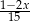 jest równa
jest równa
A) 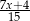 B)
B) 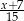 C)
C) 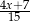 D)
D) 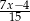
Punkt o współrzędnych 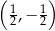 należy do wykresu funkcji logarytmicznej opisanej wzorem
należy do wykresu funkcji logarytmicznej opisanej wzorem
A) 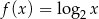 B)
B) 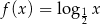 C)
C) 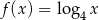 D)
D) 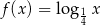
Jeżeli wiadomo, że punkt 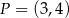 należy do wykresu funkcji
należy do wykresu funkcji 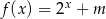 , to
, to
A) 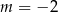 B)
B) 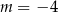 C)
C) 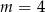 D)
D) 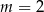
Rozwiązaniem równania 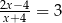 (
(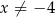 ) jest liczba
) jest liczba
A) 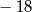 B)
B) 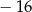 C) 16 D) 18
C) 16 D) 18
Jeżeli argument funkcji 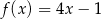 wzrośnie o 5, to wartość funkcji wzrośnie o
wzrośnie o 5, to wartość funkcji wzrośnie o
A) 18 B) 19 C) 20 D) 21
W układzie współrzędnych dane są punkty 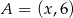 ,
, 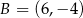 oraz
oraz 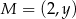 . Jeżeli punkt
. Jeżeli punkt 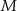 jest środkiem odcinka
jest środkiem odcinka 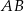 , to
, to
A) 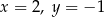 B)
B) 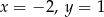 C)
C) 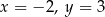 D)
D) 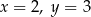
Jeśli na rysunku przedstawiony jest wykres funkcji 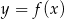 , to dziedziną funkcji
, to dziedziną funkcji 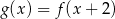 jest zbiór
jest zbiór
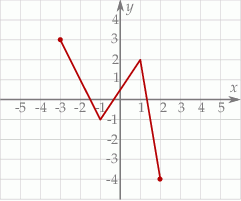
A) 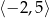 B)
B) 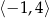 C)
C) 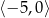 D)
D) 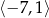
Najmniejszą liczbą całkowitą należącą do dziedziny funkcji 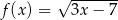 jest liczba
jest liczba
A) 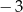 B)
B) 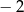 C) 2 D) 3
C) 2 D) 3
Jeśli wiadomo, że wierzchołek funkcji 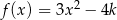 należy do prostej
należy do prostej 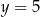 , to wartość liczbowa współczynnika
, to wartość liczbowa współczynnika 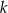 jest równa
jest równa
A) 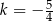 B)
B) 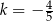 C)
C) 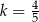 D)
D) 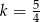
Liczbę 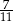 przybliżono z dokładnością do
przybliżono z dokładnością do 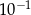 . Błąd względny tego przybliżenia jest równy
. Błąd względny tego przybliżenia jest równy
A) 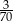 B)
B) 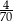 C)
C) 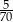 D)
D) 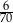
Jeśli w ciągu arytmetycznym 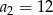 i
i 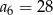 , to
, to
A) 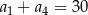 B)
B) 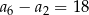 C)
C) 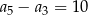 D)
D) 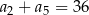
Jeśli 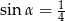 , to długość przyprostokątnej
, to długość przyprostokątnej  danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
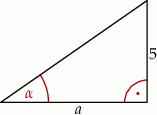
A) 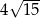 B)
B) 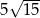 C)
C) 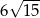 D)
D) 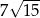
Tangens kąta ostrego  jest równy 0,6. Wówczas
jest równy 0,6. Wówczas
A) 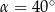 B)
B) 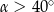 C)
C) 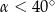 D)
D) 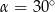
Miara kąta wpisanego w okrąg jest o 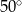 mniejsza od miary kąta środkowego opartego na tym samym łuku. Zatem miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Zatem miara kąta wpisanego jest równa
A) 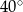 B)
B) 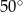 C)
C) 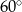 D)
D) 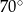
Pole równoległoboku o kącie ostrym równym 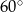 i długości boków wychodzących z wierzchołka tego kąta równych 6 i 8 jest równe
i długości boków wychodzących z wierzchołka tego kąta równych 6 i 8 jest równe
A) 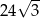 B)
B) 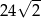 C) 24 D)
C) 24 D) 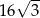
Funkcja liniowa 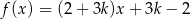 nie ma miejsc zerowych dla
nie ma miejsc zerowych dla
A) 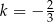 B)
B) 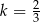 C)
C) 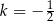 D)
D) 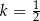
Jeżeli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 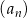 określona jest wzorem
określona jest wzorem 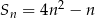 , to wartość piątego wyrazu tego ciągu jest równa
, to wartość piątego wyrazu tego ciągu jest równa
A) 33 B) 35 C) 60 D) 95
Dwa sąsiednie kąty równoległoboku różnią się o 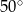 . Kąt ostry tego równoległoboku ma miarę
. Kąt ostry tego równoległoboku ma miarę
A) 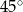 B)
B) 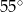 C)
C) 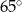 D)
D) 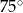
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 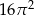 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 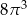 B)
B) 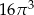 C)
C) 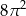 D)
D) 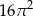
Promień podstawy stożka o objętości 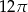 i wysokości 4 jest równy
i wysokości 4 jest równy
A) 1 B) 3 C) 6 D) 9
Miara kąta  (patrz rysunek obok) jest równa
(patrz rysunek obok) jest równa
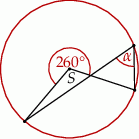
A) 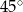 B)
B) 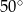 C)
C) 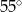 D)
D) 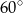
Ze zbioru kolejnych liczb naturalnych 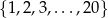 losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
A) 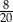 B)
B) 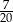 C)
C) 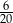 D)
D) 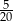
Zadania otwarte
Rozwiąż nierówność 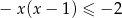 .
.
Uzasadnij, że nie istnieją dwie liczby rzeczywiste, których suma jest równa 4, a ich iloczyn jest równy 5.
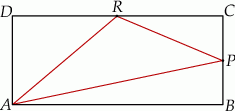
W prostokącie 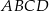 punkt
punkt 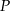 jest środkiem boku
jest środkiem boku 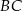 , a punkt
, a punkt 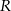 jest środkiem boku
jest środkiem boku 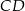 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 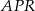 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 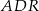 oraz
oraz 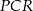 .
.
Dany jest trójkąt prostokątny o polu 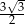 i kącie ostrym
i kącie ostrym 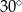 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Z punktu leżącego na okręgu o promieniu 5 poprowadzono dwie prostopadłe cięciwy. Różnica ich długości jest równa 2. Oblicz długości tych cięciw.
Dany jest trójmian kwadratowy 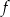 o współczynniku 3 przy najwyższej potędze
o współczynniku 3 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 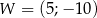 . Wyznacz
. Wyznacz 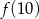 .
.
Przekątna graniastosłupa prawidłowego czworokątnego o długości 10 cm jest nachylona do płaszczyzny podstawy pod kątem 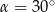 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Ze zbioru 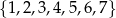 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 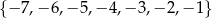 liczbę
liczbę 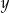 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 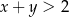 .
.
Trzy liczby tworzą ciąg arytmetyczny. Ich suma jest równa 15. Jeśli pierwszą i trzecią liczbę pozostawimy bez zmian, a drugą pomniejszymy o jeden to otrzymamy trzy kolejne wyrazy ciągu geometrycznego. Oblicz wyrazy ciągu arytmetycznego.

