/Szkoła średnia/Zadania maturalne/Matura 2019/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa I 23 maja 2018 Czas pracy: 170 minut
Zadania zamknięte
Dane są zbiory: 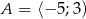 oraz
oraz 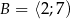 . Zbiór
. Zbiór 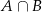 zaznaczony jest na rysunku:
zaznaczony jest na rysunku:
![]()
Liczba 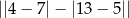 jest równa
jest równa
A) 29 B) 5 C) 7 D) 11
Odwrotnością liczby 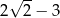 jest
jest
A) 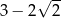 B)
B) 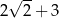 C)
C) 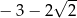 D)
D) 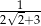
Liczba 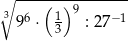 jest równa
jest równa
A) 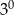 B)
B) 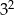 C)
C) 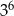 D)
D) 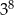
Liczba 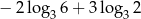 jest równa
jest równa
A) 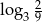 B)
B) 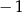 C)
C) 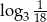 D)
D) 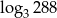
Liczba 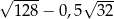 jest równa
jest równa
A) 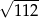 B)
B) 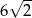 C)
C) 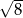 D)
D) 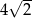
Koszt uczestnictwa w obozie sportowym w 2018 r. wynosi 1620 zł. Wzrósł on w stosunku do kosztu z 2017 r. o 35%. Koszt uczestnictwa w obozie w 2017 r. wynosił
A) 1215 zł B) 1053 zł C) 1200 zł D) 567 zł
Wartość wyrażenia 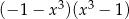 dla
dla 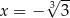 jest równa
jest równa
A) 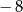 B) 2 C)
B) 2 C) 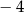 D)
D) 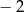
Do zbioru rozwiązań równania 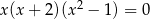 nie należy liczba
nie należy liczba
A) 0 B) 1 C) 2 D) 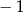
Wartość wyrażenia 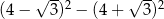 wynosi
wynosi
A) 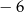 B)
B) 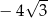 C) 6 D)
C) 6 D) 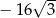
Marta oszacowała, że wyda na zakupy około 50 zł. W rzeczywistości zapłaciła 48 zł. Błąd względny, jaki popełniła szacując wartość zakupów wynosi:
A) 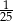 B)
B) 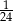 C) 2 D)
C) 2 D) 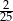
Dany jest zbiór 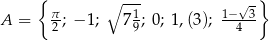 . Liczb wymiernych w zbiorze
. Liczb wymiernych w zbiorze 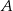 jest
jest
A) pięć B) dwie C) trzy D) cztery
Układ równań 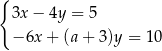 jest sprzeczny dla
jest sprzeczny dla
A) 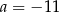 B)
B) 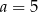 C)
C) 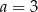 D)
D) 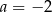
Odcinek 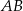 jest średnicą okręgu (rysunek).
jest średnicą okręgu (rysunek).
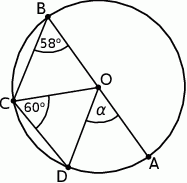
Miara kąta  jest równa
jest równa
A) 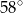 B)
B) 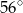 C)
C) 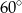 D)
D) 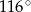
Długości boków trójkąta nie mogą być równe:
A) 3, 4, 4 B) 3, 4, 5 C) 3, 4, 2 D) 3, 4, 8
Dwa dłuższe boki trójkąta prostokątnego mają długości 3 cm oraz 4 cm. Długość najkrótszego boku tego trójkąta wynosi
A) 5 cm B) 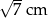 C) 2,6 cm D)
C) 2,6 cm D) 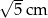
Pole koła opisanego na trójkącie prostokątnym o bokach długości 10, 24, 26 jest równe
A) 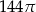 B)
B) 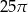 C)
C) 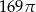 D)
D) 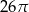
Trójkąty 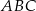 oraz
oraz 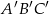 są podobne. Obwód trójkąta
są podobne. Obwód trójkąta 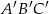 jest równy 12, a jego pole 6. Jeżeli pole trójkąta
jest równy 12, a jego pole 6. Jeżeli pole trójkąta 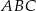 jest równe
jest równe 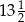 , to jego obwód wynosi
, to jego obwód wynosi
A) 18 B) 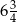 C) 27 D) 9
C) 27 D) 9
Na końcowym ramieniu kąta  (rysunek) leży punkt
(rysunek) leży punkt 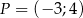 .
.
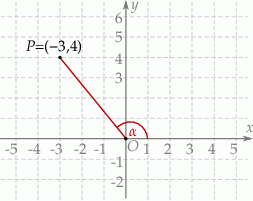
Wówczas
A) 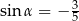 B)
B) 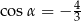 C)
C) 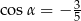 D)
D) 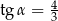
Długość boku 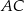 w trójkącie przedstawionym na poniższym rysunku jest równa
w trójkącie przedstawionym na poniższym rysunku jest równa
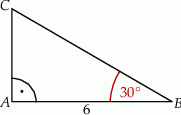
A) 3 B) 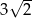 C)
C) 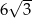 D)
D) 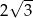
Wartość wyrażenia 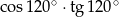 wynosi
wynosi
A) 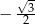 B) 1 C)
B) 1 C) 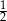 D)
D) 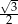
Długość okręgu wpisanego w trójkąt równoboczny wynosi 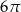 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 9 B) 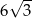 C)
C) 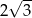 D) 6
D) 6
Zbiór 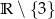 jest dziedziną funkcji
jest dziedziną funkcji
A) 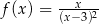 B)
B) 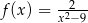 C)
C) 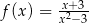 D)
D) 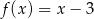
Do wykresu funkcji 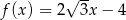 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 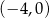 B)
B) 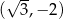 C)
C) 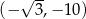 D)
D) 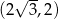
Wykres funkcji 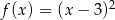 przesunięto równolegle o 2 jednostki w prawo. W wyniku tego przekształcenia otrzymano wykres funkcji
przesunięto równolegle o 2 jednostki w prawo. W wyniku tego przekształcenia otrzymano wykres funkcji
A) 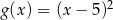 B)
B) 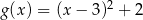 C)
C) 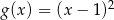 D)
D) 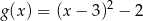
Zadania otwarte
Rozwiąż równanie 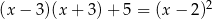 .
.
Wykaż, że jeżeli 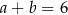 , to
, to 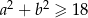 .
.
Kąt  jest ostry i
jest ostry i 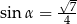 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 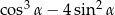 .
.
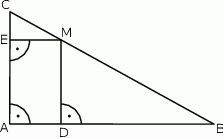
W trójkącie prostokątnym 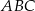 punkt
punkt 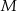 leży na przeciwprostokątnej
leży na przeciwprostokątnej 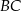 . Z punktu
. Z punktu 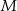 poprowadzono odcinki
poprowadzono odcinki 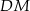 i
i 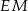 prostopadłe odpowiednio do przyprostokątnych
prostopadłe odpowiednio do przyprostokątnych 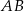 i
i 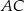 (rysunek). Udowodnij, że
(rysunek). Udowodnij, że 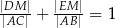 .
.
W trójkącie 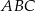 dane są:
dane są: 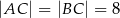 oraz
oraz 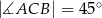 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 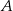 .
.
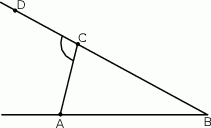
Odcinki 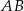 oraz
oraz 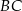 (rysunek) są równej długości. Kąt
(rysunek) są równej długości. Kąt 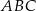 ma miarę o
ma miarę o 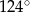 mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta
mniejszą od miary kąta do niego przyległego. Oblicz miarę kąta  .
.
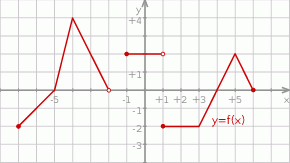
Poniżej przedstawiony jest wykres funkcji 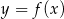 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
- dziedzinę funkcji
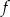 ,
, - zbiór wartości funkcji
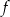 ,
, - maksymalne przedziały, w których funkcja
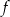 jest malejąca,
jest malejąca, - miejsca zerowe funkcji
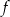 ,
, - zbiór argumentów, dla których funkcja
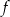 przyjmuje wartości nieujemne.
przyjmuje wartości nieujemne.
Karol zarabiał miesięcznie 4200 zł, a Jan 3800 zł. Obaj otrzymali w swoich firmach podwyżki. Podwyżka otrzymana przez Jana była o 3 punkty procentowe wyższa niż podwyżka otrzymana przez Karola. Po podwyżce obaj panowie zarabiają łącznie 9074 zł. Ile zarabia każdy z panów po podwyżce? Zapisz wszystkie obliczenia.
Wyznacz wszystkie liczby pierwsze, które należą do zbioru 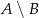 , gdzie
, gdzie 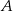 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
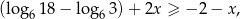
a 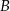 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności