/Gimnazjum/Egzamin gimnazjalny/Egzamin 2019
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 9 marca 2019 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Właściciel salonu samochodowego sporządził diagram, na którym zaznaczył miesięczną sprzedaż samochodów w okresie styczeń 2017 – grudzień 2018.
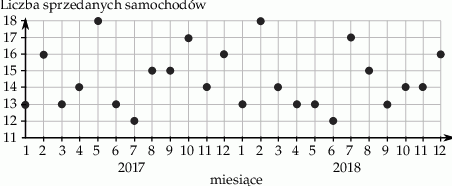
W którym z podanych okresów sprzedano najmniejszą liczbę samochodów? Wybierz właściwą odpowiedź spośród podanych.
A) styczeń 2017 – czerwiec 2017 B) lipiec 2017 – grudzień 2017
C) styczeń 2018 – czerwiec 2018 D) lipiec 2018 – grudzień 2018
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Łączna sprzedaż samochodów w dwóch kolejnych miesiącach nigdy nie przekroczyła 32 sztuk. | P | F |
| Liczba miesięcy, w których sprzedaż przekroczyła 15 samochodów była większa niż liczba miesięcy, w których sprzedaż była mniejsza niż 15 samochodów. | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 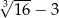 jest liczbą naturalną. jest liczbą naturalną. | P | F |
Liczba 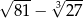 jest liczbą parzystą. jest liczbą parzystą. | P | F |
Ile jest liczb naturalnych  takich, że największy dzielnik liczby
takich, że największy dzielnik liczby  , który jest od niej mniejszy to 5?
, który jest od niej mniejszy to 5?
Wybierz odpowiedź spośród podanych.
A) 2 B) 4 C) 6 D) 3
W projekcie hotelu zaplanowano wybudowanie 30 pokojów dwuosobowych oraz 10 pokojów jednoosobowych. Po pewnym czasie projekt hotelu uległ zmianie i 10% pokojów dwuosobowych zamieniono na pokoje jednoosobowe.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba pokojów jednoosobowych zwiększyła się o
A) 3% B) 30% C) 20% D) 10%
Iloczyn 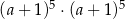 jest równy
jest równy
A) 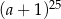 B)
B) 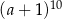 C)
C) 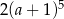 D)
D) 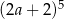
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Iloraz 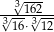 jest równy
jest równy
A) 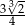 B)
B)  C)
C) 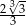 D)
D) 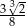
Ewa, Maciek i Julian mają razem 47 lat. Za ile lat będą mieli razem 59 lat?
Wybierz odpowiedź spośród podanych.
A) 6 B) 4 C) 3 D) 12
W windzie jechało 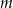 mężczyzn i
mężczyzn i 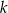 kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety.
kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Gdy winda odjechała z drugiego piętra, znajdowało się w niej
A) 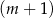 mężczyzn i
mężczyzn i 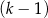 kobiet. B)
kobiet. B) 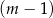 mężczyzn i
mężczyzn i 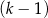 kobiet.
kobiet.
C) 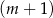 mężczyzn i
mężczyzn i 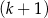 kobiet. D)
kobiet. D) 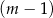 mężczyzn i
mężczyzn i 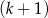 kobiet.
kobiet.
Która z nierówności jest prawdziwa? Wybierz odpowiedź spośród podanych.
A) 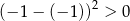 B)
B) 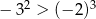 C)
C) 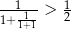 D)
D) 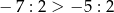
Na rysunku przedstawiono dwie bryły. Bryła I jest sześcianem o boku 5, a bryła II powstała z sześcianu o boku 5 przez usunięcie 6 sześcianów jednostkowych.
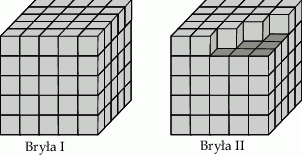
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bryła II ma większe pole powierzchni niż bryła I. | P | F |
| Objętość bryły II przekracza 90% objętości bryły I | P | F |
.
Na rysunku przedstawiono siatkę nietypowej dwunastościennej kostki do gry. Rzucamy jeden raz taką kostką.
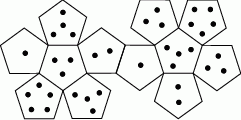
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek większej od 3 jest mniejsze od 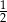 . . | P | F |
W układzie współrzędnych zaznaczono dwa wierzchołki kwadratu 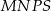 , które nie należą do tego samego boku.
, które nie należą do tego samego boku.
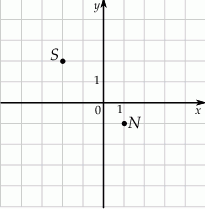
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dwa pozostałe wierzchołki tego kwadratu mają współrzędne
A) 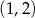 i
i 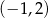 B)
B) 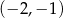 i
i 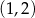 C)
C) 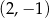 i
i 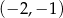 D)
D) 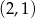 i
i 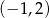
Maturzysta na rozwiązanie testu składającego się z 36 zadań przeznaczył 3 godziny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia liczba sekund przeznaczonych na jedno zadanie jest równa
A) 300 B) 240 C) 30 D) 5
Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.
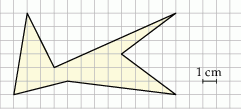
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego wielokąta jest równe
A) 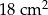 B)
B) 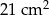 C)
C) 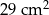 D)
D) 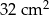
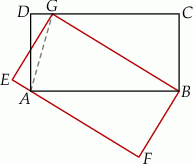
Na boku 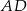 kwadratu
kwadratu 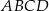 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 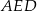 . Punkt
. Punkt 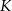 jest środkiem odcinka
jest środkiem odcinka 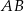 , a punkt
, a punkt 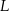 środkiem odcinka
środkiem odcinka 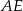 .
.
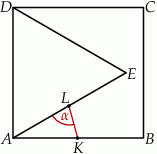
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta  jest równa
jest równa
A) 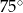 B)
B) 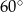 C)
C) 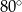 D)
D) 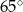
Dany jest trójkąt prostokątny 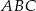 o przyprostokątnych długości 30 cm i 40 cm.
o przyprostokątnych długości 30 cm i 40 cm.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Przeciwprostokątna trójkąta 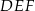 podobnego do trójkąta
podobnego do trójkąta 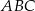 w skali 1:2 ma długość
w skali 1:2 ma długość
A) 15 cm B) 20 cm C) 25 cm D) 50 cm
Pole rombu jest równe 36, a jedna z jego przekątnych jest dwa razy krótsza od drugiej.
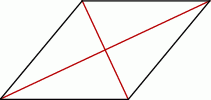
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt ostry rombu ma miarę 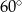 | P | F |
Bok rombu ma długość 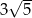 . . | P | F |
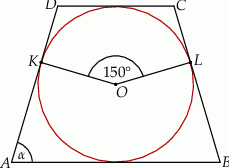
Na rysunku przedstawiono okrąg o środku 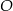 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 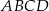 . Ramiona
. Ramiona 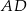 i
i 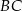 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 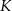 i
i 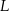 . Kąt wypukły
. Kąt wypukły 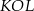 ma miarę
ma miarę 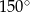 .
.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara  kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa
A) 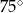 B)
B) 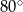 C)
C) 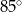 D)
D) 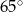
Pole podstawy stożka jest równe 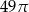 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy.
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tworząca tego stożka ma długość
A) 7 B) 10,5 C) 21 D) 14
Zmieszano dwa gatunki kaw w stosunku 1:3 i otrzymano mieszankę w cenie 66 zł za kilogram. Po zmieszaniu tych kaw w odwrotnym stosunku otrzymano mieszankę w cenie 54 zł za kilogram. Jaka byłaby cena 1 kilograma mieszanki, gdyby zmieszano te kawy w stosunku 1:1?
Na rysunku przedstawiono dwa przystające prostokąty 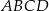 i
i 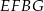 o bokach długości 5 cm i 13 cm. Oblicz długość odcinka
o bokach długości 5 cm i 13 cm. Oblicz długość odcinka 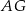 .
.
Trójkąt równoramienny o kącie 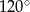 i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.