/Szkoła podstawowa/Egzamin ósmoklasisty
Egzamin Ósmoklasisty
z Matematyki (termin dodatkowy) 13 czerwca 2023 Czas pracy: 100 minut
Na diagramie przedstawiono liczbę butelek z wodą dostarczonych do sklepu osiedlowego oraz liczbę butelek z wodą sprzedanych w tym sklepie przez trzy kolejne dni: poniedziałek, wtorek i środę.
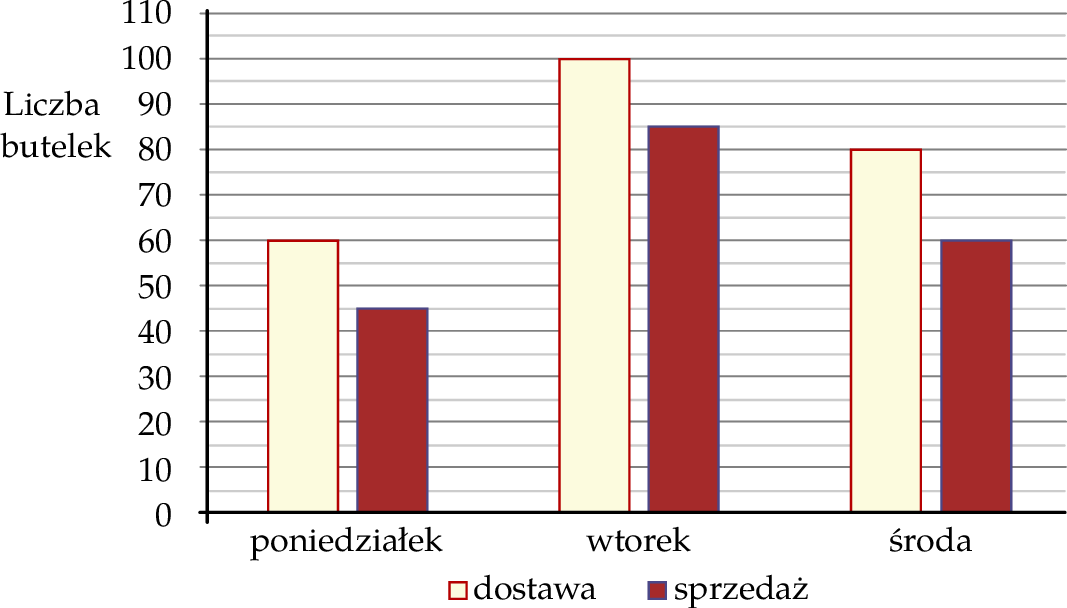
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przez te trzy dni w sklepie osiedlowym sprzedano łącznie 190 butelek z wodą. | P | F |
Liczba butelek z wodą sprzedanych w poniedziałek stanowi 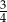 liczby butelek z wodą dostarczonych w tym dniu. liczby butelek z wodą dostarczonych w tym dniu. | P | F |
Z tasiemki o długości 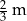 odcięto kawałek o długości pół metra. Pozostała po odcięciu część tasiemki ma długość
odcięto kawałek o długości pół metra. Pozostała po odcięciu część tasiemki ma długość
A) mniejszą od 15 cm.
B) większą od 15 cm, ale mniejszą od 16 cm.
C) równą 16 cm.
D) większą od 16 cm, ale mniejszą od 17 cm.
W pewnym zoo mieszkają słoń afrykański o masie 6 ton oraz góralek skalny o masie 3 kg. Masa słonia afrykańskiego jest większa niż masa góralka skalnego
A) 20 razy. B) 200 razy. C) 2 000 razy. D) 20 000 razy.
Dane są cztery liczby:
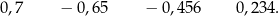
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Suma największej i najmniejszej spośród tych liczb jest równa A/B .
A) 1,35 B) 0,05
Na osi liczbowej odległość między punktami odpowiadającymi liczbom 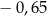 oraz
oraz 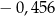 jest równa C/D .
jest równa C/D .
C) 0,194 D) 1,106
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wartość wyrażenia 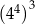 jest równa jest równa 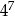 . . | P | F |
Wartości wyrażeń 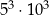 oraz oraz 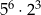 są równe. są równe. | P | F |
W naczyniu znajdowało się 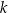 litrów wody. Marcin odlał z tego naczynia
litrów wody. Marcin odlał z tego naczynia 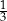 tej objętości wody, a następnie Magda odlała 3 litry wody. Objętość wody wyrażoną w litrach, która pozostała w naczyniu, opisuje wyrażenie
tej objętości wody, a następnie Magda odlała 3 litry wody. Objętość wody wyrażoną w litrach, która pozostała w naczyniu, opisuje wyrażenie
A) 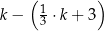 B)
B) 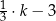 C)
C) 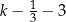 D)
D) 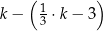
Tydzień przed rozpoczęciem zajęć student zapłacił 800 zł za kurs żeglarski. W razie rezygnacji z kursu organizator nie zwraca pełnej kwoty wpłaty, tylko oddaje jej część, zgodnie z poniższą tabelą.
| Termin rezygnacji | Wysokość zwrotu wpłaty |
| przed rozpoczęciem kursu | 95% |
| w pierwszym tygodniu kursu | 85% |
| w drugim tygodniu kursu | 70% |
| po upływie drugiego tygodnia | 5% |
Student zrezygnował z kursu w trzecim dniu zajęć. Organizator zwrócił studentowi kwotę
A) 120 zł B) 560 zł C) 680 zł D) 760 zł
Podczas spaceru w czasie każdych 10 sekund Ewa robi taką samą liczbę  kroków. Ile kroków zrobi Ewa w czasie 3 minut tego spaceru?
kroków. Ile kroków zrobi Ewa w czasie 3 minut tego spaceru?
A) 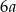 B)
B) 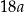 C)
C) 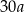 D)
D) 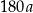
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Jest dokładnie A/B liczb naturalnych 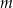 spełniających warunek
spełniających warunek 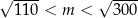 .
.
A) 7 B) 6
Są dokładnie C/D liczby naturalne 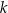 spełniające warunek
spełniające warunek 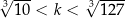 .
.
C) 4 D) 3
Spośród wszystkich liczb dwucyfrowych dodatnich losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 20 jest równe
A) 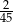 B)
B) 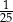 C)
C) 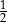 D)
D) 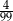
Samochód przejechał ze stałą prędkością trasę o długości 18 kilometrów w czasie 12 minut. Samochód przejechał tę trasę z prędkością
A) 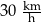 B)
B) 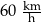 C)
C) 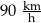 D)
D) 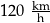
Prostokąt podzielono na dwa identyczne trapezy równoramienne i dwa trójkąty w sposób pokazany na rysunku.
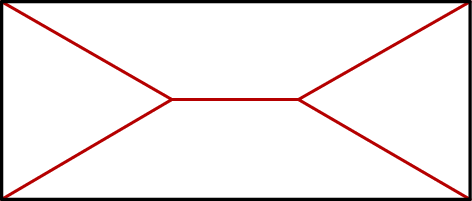
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Trójkąty, które powstały w sposób pokazany na rysunku, sąrównoramienne. | P | F |
Gdyby kąty ostre trapezów miały miarę 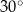 , to powstałe trójkąty byłyby równoboczne. , to powstałe trójkąty byłyby równoboczne. | P | F |
Dane są dwa równoległoboki: 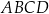 oraz
oraz 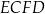 (zobacz rysunek).
(zobacz rysunek).
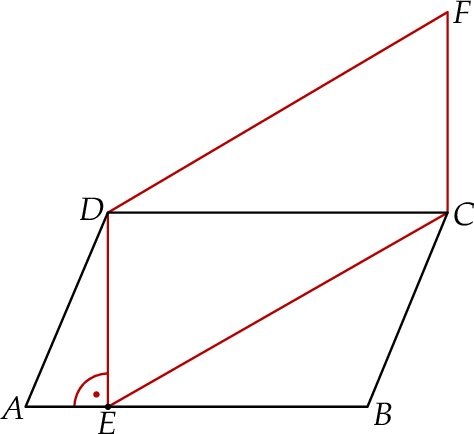
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Bok 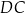 równoległoboku równoległoboku 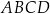 jest jedną z wysokości równoległoboku jest jedną z wysokości równoległoboku 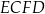 . . | P | F |
Pole równoległoboku 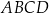 jest równe polu równoległoboku jest równe polu równoległoboku 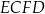 . . | P | F |
Stosunek długości trzech boków trójkąta jest równy 2 : 4 : 5. Obwód tego trójkąta jest równy 33 cm. Najkrótszy bok tego trójkąta ma długość
A) 2 cm B) 3 cm C) 6 cm D) 11 cm
Na rysunku przedstawiono graniastosłup prosty trójkątny oraz jego podstawę. Wysokość tego graniastosłupa jest równa 1 cm.

Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Pole powierzchni bocznej tego graniastosłupa jest A/B pole jednej podstawy.
A) takie samo jak B) dwa razy większe niż
Pole powierzchni całkowitej tego graniastosłupa jest równe C/D .
C) 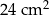 D)
D) 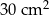
Wojtek miał 30 monet dwuzłotowych i 48 monet pięciozłotowych. Połowę monet pięciozłotowych wymienił na monety dwuzłotowe. Kwota z wymiany monet pięciozłotowych stanowiła równowartość kwoty, którą otrzymał w monetach dwuzłotowych. Oblicz, ile łącznie monet dwuzłotowych ma teraz Wojtek.
Do księgarni językowej dostarczono łącznie 240 książek napisanych w czterech różnych językach. Książek w języku włoskim było 3 razy mniej niż książek w języku niemieckim, książek w języku angielskim było 2 razy więcej niż w języku niemieckim, a książek w języku francuskim było o 20 więcej niż w języku włoskim. Oblicz, ile książek napisanych w języku francuskim dostarczono do tej księgarni.
Na rysunku przedstawiono prostokąt 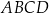 , w którym bok
, w którym bok 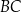 ma długość 4 cm. Na bokach prostokąta zaznaczono punkty
ma długość 4 cm. Na bokach prostokąta zaznaczono punkty 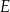 i
i 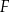 oraz narysowano odcinki
oraz narysowano odcinki 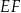 i
i 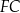 tak, że powstały dwa jednakowe trójkąty
tak, że powstały dwa jednakowe trójkąty 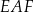 i
i 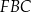 . W obu trójkątach zaznaczono kąty o takiej samej mierze
. W obu trójkątach zaznaczono kąty o takiej samej mierze  . Odcinek
. Odcinek 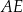 ma długość 3 cm.
ma długość 3 cm.
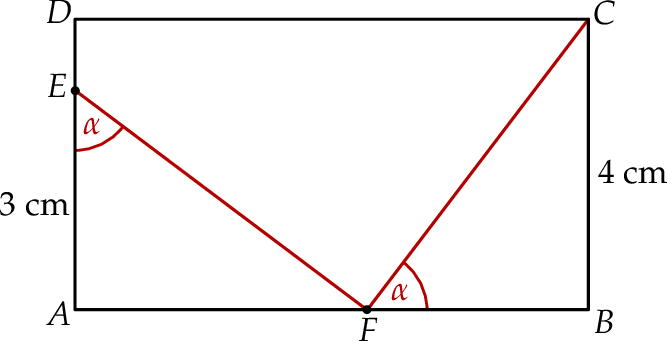
Oblicz pole prostokąta 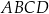 .
.
Powierzchnia kartonu ma kształt prostokąta o wymiarach 8 cm i 15 cm. W czterech rogach tego kartonu wycięto kwadraty o boku 2,5 cm. Z pozostałej części złożono pudełko.

Oblicz objętość tego pudełka.

