/Szkoła podstawowa/Egzamin ósmoklasisty
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 7 maja 2022 Czas pracy: 100 minut
W szkole Adama w gazetce szkolnej ukazał się artykuł, dotyczący wyboru przez ósmoklasistów szkoły ponadpodstawowej.
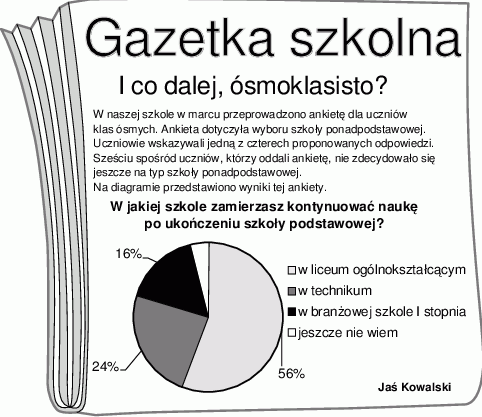
Poniżej zapisano trzy informacje.
I. Ankietę oddało łącznie 120 uczniów.
II. Ponad 80 spośród ankietowanych osób zamierza kontynuować naukę w liceum.
III. Łącznie mniej niż połowa uczniów biorących udział w ankiecie zamierza kontynuować naukę w technikum lub w branżowej szkole.
Które z informacji – I, II, III – wynikają z analizy danych zamieszczonych w treści artykułu?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) Wszystkie – I, II i III.
Dane są cztery liczby 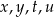 zapisane za pomocą wyrażeń arytmetycznych:
zapisane za pomocą wyrażeń arytmetycznych:
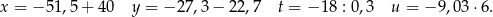
Która z tych liczb jest największa? Wybierz właściwą odpowiedź spośród podanych.
A)  B)
B) 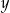 C)
C) 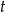 D)
D) 
W układzie współrzędnych zaznaczono punkt 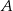 .
.
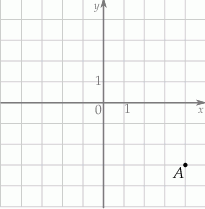
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Punkt symetryczny do punktu 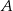 względem początku układu współrzędnych ma współrzędne
względem początku układu współrzędnych ma współrzędne
A) 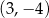 B)
B) 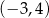 C)
C) 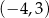 D)
D) 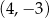
Dane są liczby: 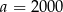 ,
, 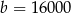 ,
, 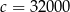 . Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Wartość wyrażenia
. Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Wartość wyrażenia 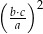 jest równa
jest równa
A) 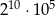 B)
B) 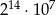 C)
C) 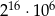 D)
D) 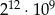
Kamil wziął udział w zajęciach przygotowawczych do konkursu plastycznego. Zajęcia składały się z 2 części. Każda część trwała tyle samo minut. Pomiędzy pierwszą a drugą częścią była 15–minutowa przerwa. Zajęcia rozpoczęły się o godzinie 13:35, a zakończyły o godzinie 15:20. Druga część zajęć rozpoczęła się o godzinie
A) 14:20 B) 14:25 C) 14:30 D) 14:35
Czy iloczyn dowolnych czterech kolejnych liczb całkowitych dwucyfrowych jest podzielny przez 10? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ wśród dowolnych czterech kolejnych liczb całkowitych | |
| A) | nie musi znajdować się liczba podzielna przez 5. |
| B) | jest co najmniej jedna liczba nieparzysta i co najmniej jedna liczba parzysta. |
| C) | jest co najmniej jedna liczba podzielna przez 5 i co najmniej jedna liczba parzysta. |
Cena brutto = cena netto + podatek VAT
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli cena netto 1 kg gruszek wzrośnie o 100%, to cena bruttoteż wzrośnie o 100%. | P | F |
| Jeżeli cena netto książki wzrośnie o 20 zł, to cena książki z 5% podatkiem VAT wzrośnie o 21 zł. | P | F |
Do liczby 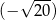 dodajemy 5.
dodajemy 5.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Otrzymany wynik jest liczbą
A) większą od 1. B) dodatnią mniejszą od 1.
C) mniejszą od 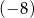 . D) ujemną większą od
. D) ujemną większą od 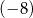 .
.
Zależność między miarą kąta wewnętrznego (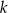 ) a liczbą boków (
) a liczbą boków ( ) wielokąta foremnego określa wzór
) wielokąta foremnego określa wzór 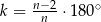 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Miara kąta wewnętrznego w 24–kącie wypukłym jest o 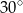 większa od miary kąta wewnętrznego ośmiokąta foremnego. większa od miary kąta wewnętrznego ośmiokąta foremnego. | P | F |
Jeżeli miara kąta wewnętrznego wielokąta foremnego jest równa 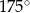 , to wielokąt ten ma 60 boków. , to wielokąt ten ma 60 boków. | P | F |
Pan Adam kupił 12 opakowań gwoździ i 6 opakowań wkrętów. Jedno opakowanie gwoździ kosztowało 4,5 zł, a średnia arytmetyczna cen wszystkich zakupionych produktów była równa 6 zł. Ile Pan Adam zapłacił za 6 opakowań wkrętów? Wybierz właściwą odpowiedź spośród podanych.
A) 6 zł B) 27 zł C) 48 zł D) 54 zł
W pewnej loterii wśród 180 losów co dziewiąty był wygrywający, a pozostałe losy były puste. Wyciągnięto 40 losów i żaden z nich nie był wygrywający.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Na loterię przygotowano A/B losów wygrywających.
A) 20 B) 140
Wyciągnięto jeszcze jeden los. Prawdopodobieństwo tego, że będzie to los wygrywający, wynosi C/D .
C) 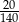 D)
D) 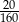
W trójkącie 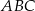 narysowano dwie wysokości:
narysowano dwie wysokości: 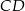 i
i 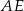 , jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy
, jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy 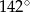 .
.
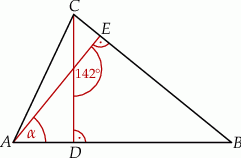
Jaką miarę ma kąt  zaznaczony na rysunku? Wybierz właściwą odpowiedź spośród podanych.
zaznaczony na rysunku? Wybierz właściwą odpowiedź spośród podanych.
A) 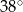 B)
B) 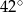 C)
C) 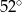 D)
D) 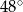
W zeszycie w linie narysowano dwa trójkąty i równoległobok w sposób pokazany na rysunku. Odległości między sąsiednimi liniami są jednakowe. Podstawy wszystkich tych figur mają taką samą długość. Pole trójkąta 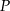 jest równe 4.
jest równe 4.
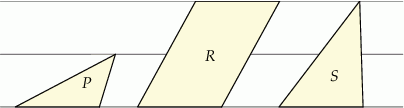
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole równoległoboku 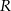 jest równe 12. jest równe 12. | P | F |
Pole trójkąta 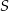 jest równe 8. jest równe 8. | P | F |
W prostopadłościennym akwarium, o wymiarach podanych na rysunku, woda sięga  jego wysokości.
jego wysokości.
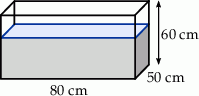
Ile litrów wody jest w akwarium?
Wybierz odpowiedź spośród podanych.
A) 16000 litrów B) 1600 litrów C) 160 litrów D) 16 litrów
Dwa sześciany – jeden o krawędzi 3 i drugi o krawędzi 4 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 150 B) 222 C) 366 D) 111
Kamil powiedział, że podzieli zgromadzone oszczędności w następujący sposób: 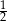 oszczędności przeznaczy na zakup roweru,
oszczędności przeznaczy na zakup roweru, 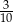 oszczędności przeznaczy na zakup deskorolki,
oszczędności przeznaczy na zakup deskorolki,  oszczędności zachowa na wakacje. Czy taki podział zgromadzonych oszczędności jest możliwy?
oszczędności zachowa na wakacje. Czy taki podział zgromadzonych oszczędności jest możliwy?
Z portu rybackiego (punkt 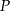 ) wypłynęły jednocześnie na połów dwa kutry: jeden na północ ze stałą prędkością 4 węzłów, drugi na wschód ze stałą prędkością 3 węzłów. Oblicz odległość między tymi kutrami po dwóch godzinach od wypłynięcia. Wynik podaj w kilometrach. Zapisz obliczenia.
) wypłynęły jednocześnie na połów dwa kutry: jeden na północ ze stałą prędkością 4 węzłów, drugi na wschód ze stałą prędkością 3 węzłów. Oblicz odległość między tymi kutrami po dwóch godzinach od wypłynięcia. Wynik podaj w kilometrach. Zapisz obliczenia.

Do rozwiązania zadania skorzystaj z informacji: 1 węzeł to 1 mila morska na godzinę, 1 mila morska = 1852 m.
Piotrek kupił 3 rodzaje ciastek: duże, średnie i małe. Duże ciastko kosztuje 4 zł za sztukę, średnie po 2 zł, a małe po 1 zł. Piotrek kupił łącznie 10 ciastek za które zapłacił 16 zł. Ile kupił dużych ciastek?
Na rysunku przedstawiono kwadrat 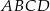 o polu
o polu 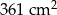 . Figurę tę podzielono na kwadrat
. Figurę tę podzielono na kwadrat 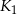 o polu
o polu 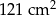 i kwadrat
i kwadrat 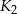 oraz figurę
oraz figurę 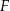 (patrz rysunek).
(patrz rysunek).
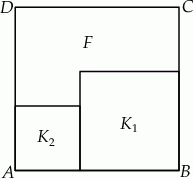
Oblicz obwód figury 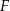 .
.

