/Szkoła podstawowa/Egzamin ósmoklasisty
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 14 maja 2022 Czas pracy: 100 minut
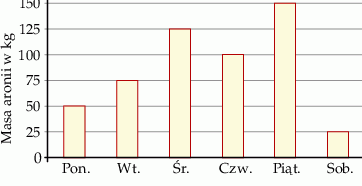
Pan Łukasz przez sześć kolejnych dni tygodnia pracował przy zbiórce aronii. Na diagramie przedstawiono wyniki jego zbiorów.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pan Łukasz zbierał średnio 85 kg aronii dziennie. | P | F |
| Gdyby pan Łukasz w sobotę zebrał dwa razy więcej owoców, to w sumie zebrałby 550 kg aronii. | P | F |
Adam i Wojtek mają razem 82 cukierki. Jeżeli każdy z chłopców zje 29 cukierków, to Adam będzie miał trzy razy mniej cukierków niż Wojtek.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli Wojtek odda Adamowi 6 cukierków, to chłopcy będą mieli taką samą liczbę cukierków. | P | F |
| Jeżeli każdy z chłopców zje 23 cukierki, to Wojtek będzie miał dwa razy więcej cukierków niż Adam. | P | F |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 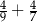 jest liczbą A/B .
jest liczbą A/B .
A) mniejszą od 1 B) większą od 1
Wartość wyrażenia 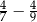 jest liczbą C/D .
jest liczbą C/D .
C) ujemną D) dodatnią
Która z poniższych nierówności jest prawdziwa? Wybierz właściwą odpowiedź spośród podanych.
A) 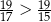 B)
B) 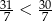 C)
C) 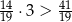 D)
D) 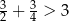
W tabeli przedstawiono informacje dotyczące cen akcji trzech firm w dwóch różnych wybranych dniach tego samego roku.
| Firma | Cena 1 akcji w dniu 1 lutego | Cena 1 akcji w dniu 31 sierpnia |
| Salceson S.A. | 15 zł | 18 zł |
| Kabanos S.A. | 24 zł | 36 zł |
| Salami S.A. | 96 zł | 64 zł |
W okresie między 1 lutego a 31 sierpnia cena akcji firmy Kabanos S.A. wzrosła o A/B .
A) 40% B) 50%
[SQREMOVE]Wartość 60 akcji firmy Salceson S.A. i 10 akcji firmy Salami S.A. w okresie od między 1 lutego a 31 sierpnia C/D .
C) zmalała D) wzrosła
Dane są trzy wyrażenia:
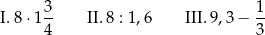
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczbami całkowitymi są wartości wyrażeń
A) I, II i III B) Tylko I i II C) Tylko II i III D) Tylko I i III
Korzystając z tego, że 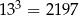 i
i 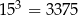 , oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
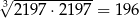 | P | F |
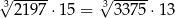 | P | F |
Informacja do zadań 8 i 9
Trójki liczb naturalnych 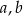 i
i  , które spełniają warunek
, które spełniają warunek 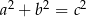 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
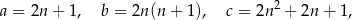
gdzie  oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (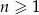 ).
).
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba 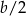 zawsze będzie A/B .
zawsze będzie A/B .
A) parzysta B) nieparzysta
Liczby 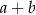 i
i  różnią się o C/D .
różnią się o C/D .
C) 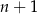 D)
D) 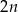
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jeżeli najmniejsza z liczb 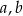 i
i  jest równa 11, to największa z tych liczb jest równa
jest równa 11, to największa z tych liczb jest równa
A) 265 B) 73 C) 145 D) 61
Wartość wyrażenia 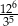 jest równa
jest równa
A) 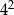 B)
B) 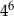 C)
C) 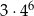 D)
D) 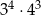
W trójkącie stosunek miar kątów jest równy 2 : 3 : 5.
Wybierz właściwą odpowiedź spośród podanych.
Trójkąt o podanych własnościach jest
A) rozwartokątny. B) prostokątny. C) ostrokątny. D) równoramienny.
Listewkę o długości 60 cm planowano pociąć na równe części. Iwona zaproponowała podział na kawałki po 5 cm i zaznaczyła na listewce czerwonym kolorem linie cięcia. Agata chciała podzielić tę samą listewkę na części po 2 cm i linie cięcia zaznaczyła na zielono. Ile razy linia czerwona pokrywała się z linią zieloną? Wybierz właściwą odpowiedź spośród podanych.
A) 5 B) 4 C) 3 D) 2
Punkty 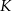 ,
, 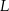 i
i 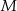 są środkami boków
są środkami boków 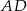 ,
, 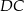 i
i 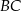 kwadratu
kwadratu 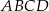 (rysunek).
(rysunek).
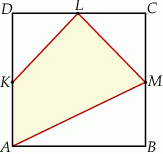
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 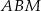 stanowi stanowi 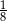 pola kwadratu pola kwadratu 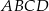 . . | P | F |
Pole czworokąta 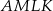 stanowi połowę pola kwadratu stanowi połowę pola kwadratu 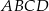 . . | P | F |
Przekątne rombu mają długości 24 i 10.
Jaka jest długość boku rombu? Wybierz odpowiedź spośród podanych.
A) 13 B) 26 C) 6,5 D) 14
Na siatce sześcianu zaznaczono jego dwie ściany 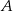 i
i 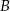 oraz jego dwie krawędzie
oraz jego dwie krawędzie 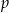 i
i 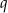 .
.
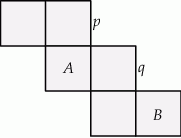
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ściany 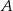 i i 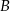 są przeciwległymi ścianami sześcianu. są przeciwległymi ścianami sześcianu. | P | F |
Krawędzie 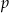 i i 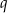 są prostopadłymi krawędziami sześcianu. są prostopadłymi krawędziami sześcianu. | P | F |
Pewną liczbę cukierków rozdzielono pomiędzy trzy osoby. Kasia otrzymała 3 razy mniej cukierków niż Zosia, a Ela 2 razy więcej niż Zosia. Uzasadnij, że Kasia otrzymała 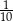 wszystkich cukierków.
wszystkich cukierków.
Ela mieszka w miejscowości Zalesie, a jej koleżanka Kasia – w miejscowości Podgaj. Ela umówiła się z Kasią w Podgaju na godzinę 14:00. Wyjechała z Zalesia na skuterze o godzinie 13:10. Średnia prędkość jazdy Eli była równa 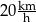 . Na kwadratowej siatce Ela przedstawiła schemat trasy, którą jechała.
. Na kwadratowej siatce Ela przedstawiła schemat trasy, którą jechała.
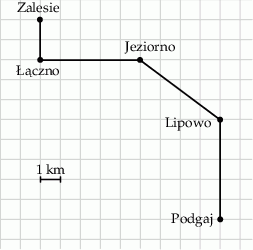
O której godzinie Ela dotarła na spotkanie z Kasią?
Antek stwierdził, że ma tylko 20 zł w skarbonce, a jego kolega Wojtek ma 160 zł. Antek postanowił co tydzień dokładać do skarbonki 2 zł, podczas gdy Wojtek co tydzień wydawał 5 zł ze swych oszczędności. Po ilu tygodniach koledzy będą mieli tyle samo pieniędzy?
Dany jest trójkąt równoramienny o bokach długości 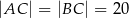 i
i 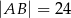 . Odcinek
. Odcinek 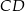 jest wysokością trójkąta
jest wysokością trójkąta 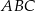 , a odcinek
, a odcinek 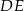 jest wysokością trójkąta
jest wysokością trójkąta 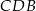 (zobacz rysunek).
(zobacz rysunek).
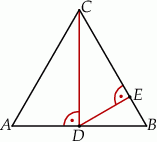
Oblicz długość odcinka 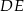 .
.

