/Szkoła podstawowa/Egzamin ósmoklasisty
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 30 marca 2019 Czas pracy: 100 minut
Informacja do zadań 1 i 2
Firma przesyłkowa Pudełko korzysta z paczkomatów do samodzielnego nadawania i odbierania przesyłek przez klientów. Firma oferuje trzy rodzaje przesyłek:
| Gabaryt | Maksymalne wymiary | Cena nadania paczki |
| A | 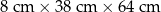 | 6,40 zł |
| B | 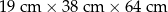 | 11,20 zł |
| C | 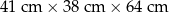 | 15,40 zł |
W tabeli zapisano wymiary jednej paczki i liczbę paczek w czterech zleceniach wysyłki
| Nr zlecenia | Wymiary 1 paczki | Liczba paczek |
| 1 | 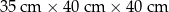 | 3 |
| 2 | 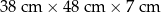 | 7 |
| 3 | 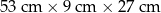 | 5 |
| 4 | 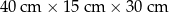 | 4 |
Ile z tych zleceń może zostać zrealizowanych w cenie niższej niż 50 zł? Wybierz właściwą odpowiedź spośród podanych.
A) Jedno. B) Dwa. C) Trzy. D) Cztery.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Maksymalna objętość paczki gabarytu B jest co najmniej dwa razy większa niż objętość paczki gabarytu A. | P | F |
| Pięć paczek gabarytu A może mieć większą całkowitą objętość niż maksymalna paczka gabarytu C. | P | F |
Dane są trzy liczby
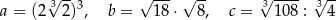
Która nierówność jest prawdziwa? Wybierz właściwą odpowiedź spośród podanych.
A) 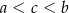 B)
B) 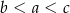 C)
C) 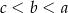 D)
D) 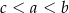
Natalia przechowuje na zewnętrznym dysku USB swoje najważniejsze pliki. Diagram przedstawia procentowy rozkład pojemności tego dysku w zależności od rodzaju przechowywanych plików.
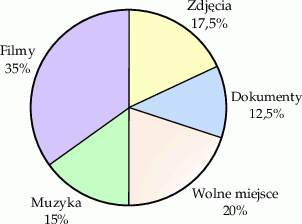
Gdyby Natalia skasowała wszystkie pliki muzyczne z tego dysku, to ilość wolnego miejsca zwiększyłaby się do 112 GB. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Filmy zajmują na tym dysku A/B .
A) 320 GB B) 112 GB
Zdjęcia zajmują na dysku o C/D więcej miejsca niż dokumenty.
C) 16 GB D) 56 GB
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wartość wyrażenia 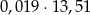 jest równa wartości wyrażenia jest równa wartości wyrażenia 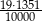 . . | P | F |
Wartość wyrażenia 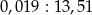 jest równa wartości wyrażenia jest równa wartości wyrażenia 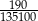 . . | P | F |
Zaokrąglenia czterocyfrowych liczb  i
i 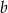 do pełnych dziesiątek są takie same.
do pełnych dziesiątek są takie same.
Czy cyfry tysięcy liczb  i
i 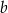 muszą być takie same? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.
muszą być takie same? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | liczby  i i 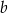 różnią się o co najwyżej 10. różnią się o co najwyżej 10. |
| B) | pomiędzy liczbami  i i 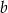 może być liczba podzielna przez 1000. może być liczba podzielna przez 1000. |
| C) | zaokrąglenia tych liczb do pełnych tysięcy też są równe. |
Na rysunku przedstawiono fragment podłogi pokrytej kaflami w kształcie kwadratów i kaflami w kształcie jednakowych prostokątów (patrz rysunek I). Na podłodze tej położono prostokątny dywan (patrz rysunek II).
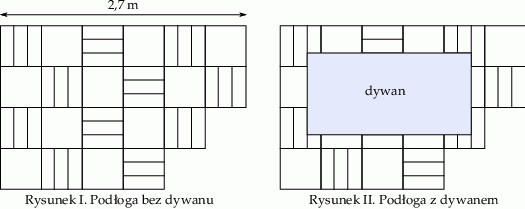
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dywan ma pole powierzchni większe niż 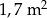 | P | F |
Dywan ma wymiary 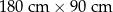 . . | P | F |
Narysowany diagram należy wypełnić liczbami naturalnymi tak, aby każda liczba była równa iloczynowi dwóch liczb napisanych bezpośrednio nad nią.
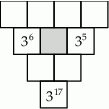
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
W zacieniowane pole należy wpisać liczbę 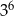 . . | P | F |
Iloczyn wszystkich liczb w tablicy jest równy 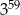 . . | P | F |
Kamil ma trzy siostry i jednego brata bliźniaka. Średnia wieku wszystkich dzieci w tej rodzinie jest równa 10,2 roku, a średnia wieku samych dziewcząt jest równa 7 lat. Ile lat ma Kamil?
Wybierz właściwą odpowiedź spośród podanych.
A) 30 B) 17 C) 15 D) 21
Rzucamy ośmiokrotnie standardową sześcienną kostką do gry. Liczba  jest iloczynem wszystkich otrzymanych liczb oczek. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest iloczynem wszystkich otrzymanych liczb oczek. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba  może być równa 35. może być równa 35. | P | F |
Liczba  może być równa 1024. może być równa 1024. | P | F |
O liczbach 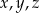 wiemy, że kwadrat ich iloczynu jest o 20% większy od odwrotności ich sumy.
wiemy, że kwadrat ich iloczynu jest o 20% większy od odwrotności ich sumy.
Która równość poprawnie opisuje zależność wiążącą liczby 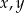 i
i  ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) 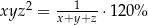 B)
B) 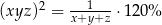
C) 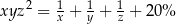 D)
D) 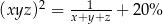
Odcinek 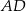 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 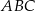 , w którym przyprostokątna
, w którym przyprostokątna 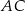 ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry 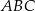 ma miarę
ma miarę 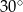 (zobacz rysunek).
(zobacz rysunek).
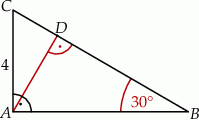
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Kąt 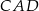 ma miarę A/B .
ma miarę A/B .
A) 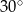 B)
B) 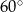
Odcinek 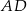 ma długość C/D .
ma długość C/D .
C) 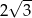 D)
D) 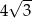
W układzie współrzędnych zaznaczono dwa punkty: 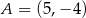 i
i 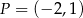 . Punkt
. Punkt 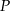 jest środkiem odcinka
jest środkiem odcinka 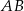 .
.
Jakie współrzędne ma punkt B? Wybierz właściwą odpowiedź spośród podanych.
A) 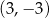 B)
B) 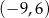 C)
C) 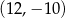 D)
D) 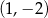
Przekątne prostokąta 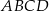 przedstawionego na rysunku przecinają się pod kątem
przedstawionego na rysunku przecinają się pod kątem 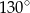 .
.
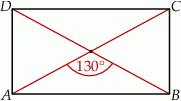
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 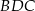 ma miarę ma miarę 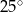 . . | P | F |
Kąt 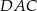 ma miarę ma miarę 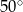 . . | P | F |
Ewa z sześciennych klocków o krawędzi długości 3 cm skleiła kilka brył o kształcie pokazanym na rysunku.
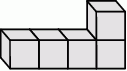
Z czterech takich brył Ewa skleiła graniastosłup prawidłowy czworokątny.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wysokość tego graniastosłupa jest równa A/B .
A) 12 cm B) 15 cm
Pole powierzchni bocznej utworzonego graniastosłupa jest równe C/D .
C) 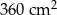 D)
D) 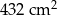
Dane są trzy wyrażenia:
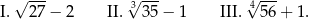
Wartości których wyrażeń są mniejsze od 4? Wybierz właściwą odpowiedź spośród podanych.
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
W pewnym mieście naukę w klasach pierwszych szkół podstawowych rozpoczęło 1854 uczniów urodzonych w roku 2012. Wykaż, że wśród tych uczniów jest co najmniej sześcioro uczniów z taką samą datą urodzenia.
Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest prostokątem o bokach 6 cm i 9 cm, a druga – prostokątem o bokach 9 cm i 12 cm.
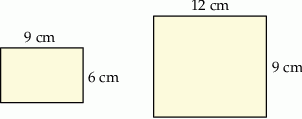
Oblicz pole powierzchni całkowitej prostopadłościanu o takich wymiarach.
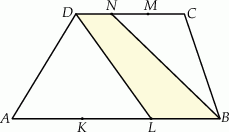
Punkty 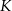 i
i 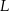 dzielą podstawę
dzielą podstawę 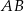 trapezu
trapezu 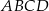 na trzy równe części, a punkty
na trzy równe części, a punkty 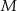 i
i 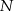 dzielą podstawę
dzielą podstawę 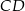 tego trapezu na trzy równe części. Pole czworokąta
tego trapezu na trzy równe części. Pole czworokąta 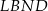 jest równe
jest równe 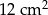 . Oblicz pole trapezu
. Oblicz pole trapezu 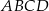 .
.
Pani Katarzyna planuje wymienić waluty w kantorze. W poniższej tabeli przedstawiono ceny skupu i sprzedaży jednego dolara (USD) i jednego euro (EUR).
| Cena skupu | Cena sprzedaży | |
| USD | 3,6 zł | 3,8 zł |
| EUR | 4,2 zł | 4,5 zł |
Pani Katarzyna chce sprzedać 650 dolarów i kupić za otrzymane pieniądze euro. Ile euro kupi Pani Katarzyna?
Hugo wybrał się do kolegi mieszkającego w Tczewie. Tata podwiózł go na przystanek pociągu, potem Hugo czekał na przyjazd pociągu. Po przyjeździe do Tczewa, Hugo doszedł pieszo do mieszkania kolegi. Na wykresie w sposób uproszczony przedstawiono zależność prędkości, z jaką poruszał się Hugo, od czasu.
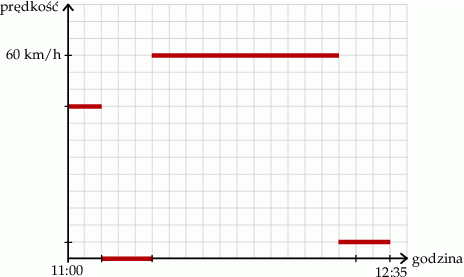
Oblicz długość trasy pokonanej przez Huga od wyjścia z domu do chwili dotarcia do mieszkania kolegi.
Wśród uczestników obozu sportowego było o 28 chłopców więcej niż dziewcząt. W trakcie gry terenowej wszystkich chłopców podzielono na grupy siedmioosobowe, a wszystkie dziewczynki na grupy pięcioosobowe. W ten sposób powstały o 2 więcej grupy składających się z dziewcząt, niż jest grup składających się z chłopców. Ilu chłopców i ile dziewcząt brało udział w tym obozie?

