/Szkoła podstawowa/Egzamin ósmoklasisty
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 20 kwietnia 2024 Czas pracy: 100 minut
Wśród pewnej grupy osób przeprowadzono ankietę. Jedno z pytań brzmiało: Jaki jest twój ulubiony dzień tygodnia?. Każdy ankietowany wskazał tylko jeden dzień tygodnia. Rozkład udzielonych odpowiedzi na to pytanie przedstawiono na diagramie.
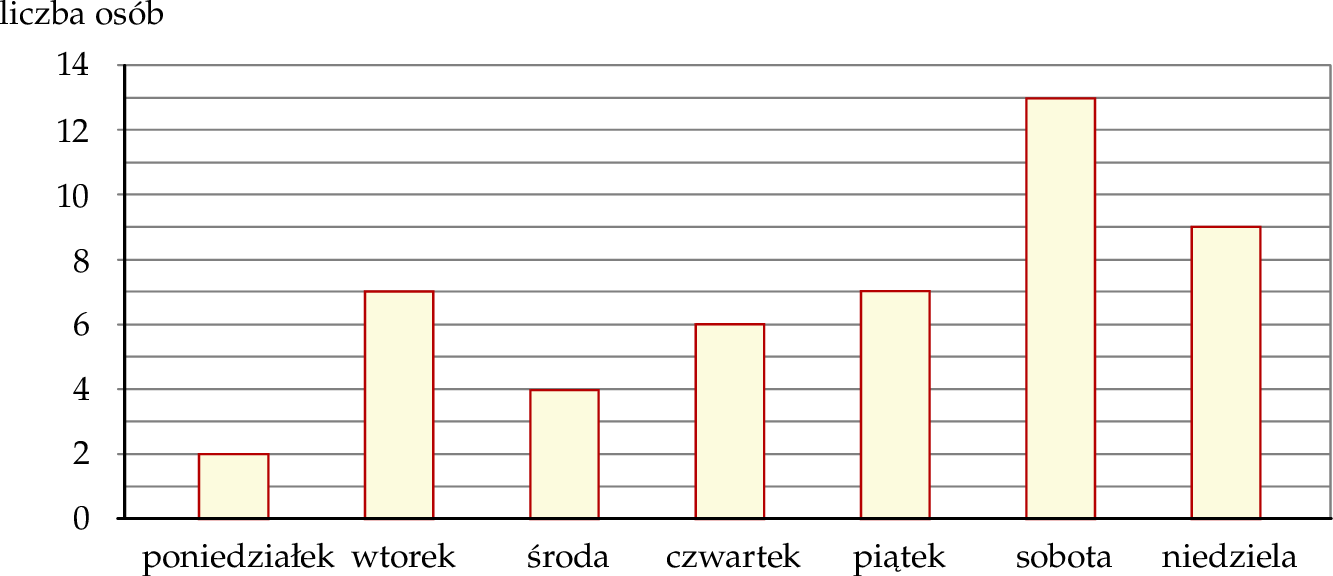
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Niedziela jest ulubionym dniem tygodnia dla mniej niż  liczby osób ankietowanych. liczby osób ankietowanych. | P | F |
| Ponad 50% ankietowanych osób jako ulubiony dzień tygodnia wskazało wtorek, czwartek lub sobotę. | P | F |
Dostęp do pliku jest chroniony hasłem 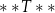 złożonym z dwóch liczb dwucyfrowych oddzielonych literą
złożonym z dwóch liczb dwucyfrowych oddzielonych literą 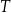 . Pierwsza liczba hasła to najmniejszy wspólny mianownik ułamków
. Pierwsza liczba hasła to najmniejszy wspólny mianownik ułamków 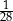 i
i 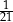 , a druga to reszta z dzielenia pierwszej liczby przez 29. Jakie jest hasło do pliku?
, a druga to reszta z dzielenia pierwszej liczby przez 29. Jakie jest hasło do pliku?
A) 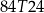 B)
B) 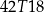 C)
C) 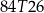 D)
D) 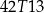
Liczby:  ,
, 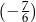 ,
, 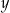 , są uporządkowane rosnąco. Liczba
, są uporządkowane rosnąco. Liczba 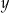 jest o 0,5 większa od
jest o 0,5 większa od 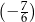 , a liczba
, a liczba 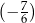 jest o 0,5 większa od liczby
jest o 0,5 większa od liczby  . Jakie wartości mają liczby
. Jakie wartości mają liczby  i
i 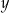 ?
?
A) 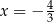 i
i 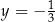 B)
B) 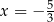 i
i 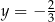
C) 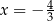 i
i 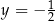 D)
D) 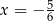 i
i 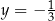
Ewa ułożyła na półce książki w sposób pokazany na rysunku.
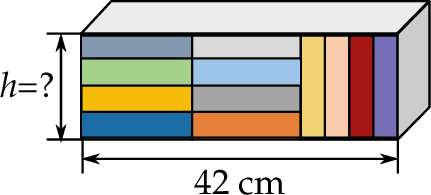
Wszystkie książki były jednakowych rozmiarów i półka została całkowicie przez nie wypełniona. Jaka jest wysokość tej półki?
A) 12 cm B) 15 cm C) 14 cm D) 16 cm
Dane są trzy liczby:
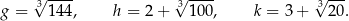
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 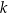 jest większa od liczby jest większa od liczby 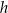 . . | P | F |
Liczba 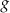 nie jest największą spośród liczb: nie jest największą spośród liczb: 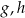 i i 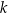 . . | P | F |
W sadzie rosną drzewa owocowe: grusze i jabłonie. Liczba jabłoni jest o 40% większa od liczby grusz. Grusz jest o 30 mniej niż jabłoni. Ile jabłoni rośnie w tym sadzie?
A) 90 B) 105 C) 75 D) 125
Liczbę 400 można zapisać w postaci 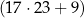 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Resztą z dzielenia liczby 400 przez 23 jest 17. | P | F |
| Jeśli liczbę 400 zwiększymy o 8, to otrzymamy liczbę podzielną przez 17. | P | F |
Połowę liczby  zmniejszono o 3, a następnie do otrzymanego wyniku dodano dwukrotność liczby
zmniejszono o 3, a następnie do otrzymanego wyniku dodano dwukrotność liczby 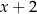 . W wyniku tych działań otrzymano wyrażenie
. W wyniku tych działań otrzymano wyrażenie
A) 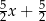 B)
B) 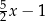
C) 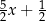 D)
D) 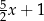
Dane są liczby
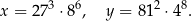
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Iloczyn 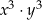 jest równy A/B .
jest równy A/B .
A) 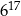 B)
B) 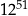
Iloraz 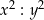 jest równy C/D .
jest równy C/D .
C) 144 D) 12
Na planie miasta odległość w linii prostej od punktu oznaczającego przystanek autobusowy Uniwersytet do punktu oznaczającego przystanek autobusowy Muzeum jest równa 12 cm. Plan miasta został wykonany w skali 1 : 5 000.
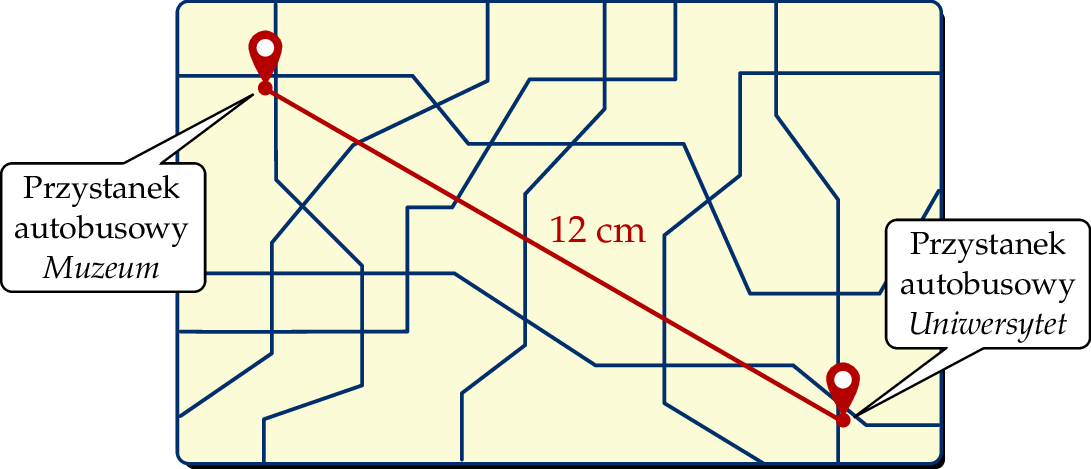
Odległość w linii prostej w terenie między tymi przystankami jest równa
A) 2 400 m B) 600 m C) 3 200 m D) 6 000m
W pewnym rombie jeden z kątów wewnętrznych ma miarę 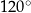 . Obwód tego rombu jest równy 28 cm. Dłuższa przekątna tego rombu ma długość
. Obwód tego rombu jest równy 28 cm. Dłuższa przekątna tego rombu ma długość
A) 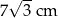 B) 7 cm C)
B) 7 cm C) 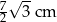 D) 14 cm
D) 14 cm
Dany jest trapez prostokątny 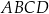 , w którym
, w którym 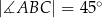 . Punkty
. Punkty 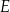 i
i 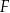 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 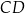 i
i 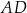 .
.

Długość odcinka 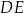 jest równa 6, a długość odcinka
jest równa 6, a długość odcinka 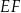 jest równa 10. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest równa 10. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trapezu 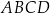 jest liczbą całkowitą. jest liczbą całkowitą. | P | F |
Pole trapezu 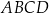 jest równe 320. jest równe 320. | P | F |
Na rysunku przedstawiono równoległobok 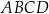 , który nie jest prostokątem. Długości boków tego równoległoboku opisano za pomocą wyrażeń algebraicznych.
, który nie jest prostokątem. Długości boków tego równoległoboku opisano za pomocą wyrażeń algebraicznych.
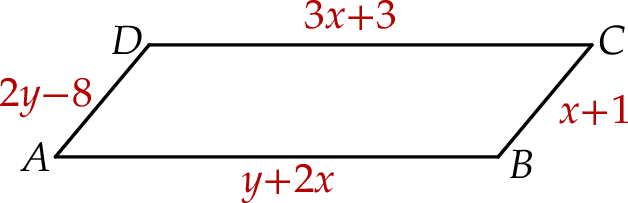
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole równoległoboku 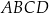 jest równe 48. jest równe 48. | P | F |
Obwód równoległoboku 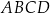 jest równy 32. jest równy 32. | P | F |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 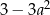 dla
dla 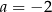 jest równa A/B .
jest równa A/B .
A) 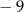 B) 15
B) 15
Wyrażenie 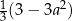 można przekształcić do postaci C/D .
można przekształcić do postaci C/D .
C) 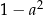 D)
D) 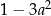
Na rysunku przedstawiono trzy figury: kwadrat 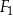 , prostokąt
, prostokąt 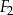 i prostokąt
i prostokąt 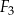 , oraz podano ich wymiary.
, oraz podano ich wymiary.

Czy z figur 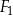 ,
, 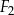 ,
, 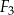 można ułożyć, bez rozcinania tych figur, kwadrat
można ułożyć, bez rozcinania tych figur, kwadrat 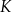 o obwodzie 28 cm? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
o obwodzie 28 cm? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | suma obwodów figur 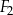 i i 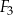 jest równa obwodowi kwadratu jest równa obwodowi kwadratu 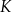 . . |
| B) | suma pól figur 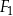 , , 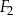 i i 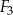 nie jest równa nie jest równa 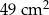 . . |
| C) | suma długości dowolnych boków figur 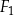 , , 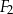 i i 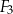 nie jest równa 7 cm. nie jest równa 7 cm. |
W cukierni Lukier drożdżówka jest o 2 zł tańsza od jagodzianki i o 1 zł droższa od pączka. Za 7 pączków, 3 drożdżówki i 6 jagodzianek zapłacono w tej cukierni 109 zł. Oblicz, ile kosztuje jeden pączek w cukierni Lukier.
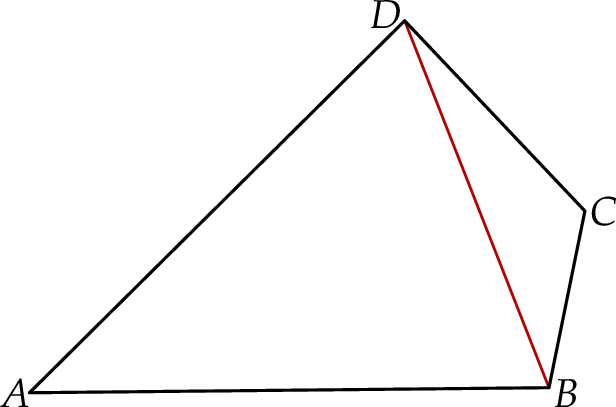
W czworokącie 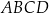 o polu
o polu 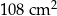 przekątna
przekątna 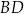 ma długość 12 cm i dzieli ten czworokąt na dwa trójkąty:
ma długość 12 cm i dzieli ten czworokąt na dwa trójkąty: 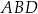 i
i 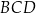 (zobacz rysunek). Wysokość trójkąta
(zobacz rysunek). Wysokość trójkąta 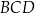 poprowadzona z wierzchołka
poprowadzona z wierzchołka 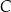 do prostej
do prostej 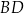 jest równa 3 cm.
jest równa 3 cm.
Oblicz wysokość trójkąta 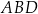 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka 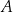 do prostej
do prostej 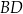 .
.
Marta miała łącznie 90 piłeczek, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich są – odpowiednio – kolejnymi liczbami podzielnymi przez 6. Marta rozdzieliła wszystkie piłeczki na sześć identycznych zestawów, przy czym w każdym z nich znalazły się piłeczki w trzech kolorach. Oblicz, ile piłeczek czerwonych, ile – zielonych, a ile – niebieskich było w jednym zestawie.
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest prostokąt.
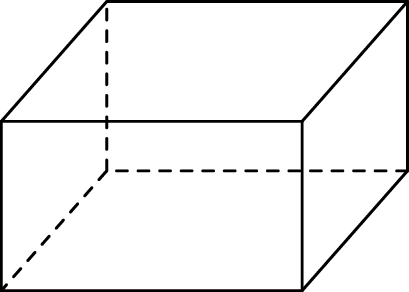
Jeden z boków tego prostokąta ma długość 16 cm, a długość jego przekątnej jest równa 20 cm. Przekątna najmniejszej ściany bocznej graniastosłupa ma długość 15 cm. Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.

