/Szkoła podstawowa/Egzamin ósmoklasisty
Próbny Egzamin Ósmoklasisty
z Matematyki CKE 18 marca 2021 Czas pracy: 100 minut
W szkole Adama w gazetce szkolnej ukazał się artykuł, dotyczący wyboru przez ósmoklasistów szkoły ponadpodstawowej.
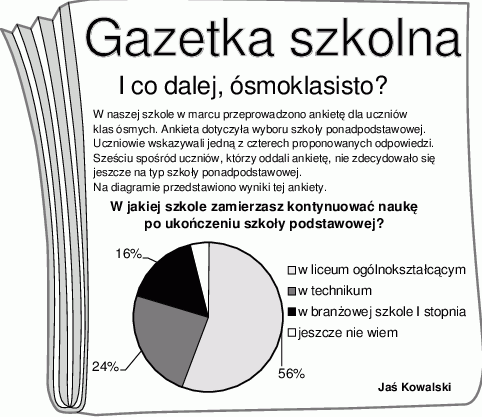
Poniżej zapisano trzy prawdziwe informacje.
I. Ankietę oddało łącznie 150 uczniów.
II. W ankiecie wzięli udział wszyscy uczniowie klas ósmych.
III. Łącznie mniej niż połowa uczniów biorących udział w ankiecie zamierza kontynuować naukę w technikum lub w branżowej szkole.
Które z informacji – I, II, III – wynikają z analizy danych zamieszczonych w treści artykułu?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) Wszystkie – I, II i III.
Piłki tenisowe zapakowano do 186 jednakowych pudełek. Do każdego z tych pudełek włożono po 6 piłek. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba wszystkich spakowanych piłek jest podzielna przez 4. | P | F |
| Wszystkie te piłki można byłoby spakować do większych pudełek – po 9 piłek w każdym. | P | F |
Która z poniższych nierówności jest prawdziwa? Wybierz właściwą odpowiedź spośród podanych. Wybierz właściwą odpowiedź spośród podanych.
A) 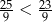 B)
B) 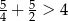 C)
C) 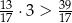 D)
D) 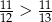
Dane są trzy wyrażenia:
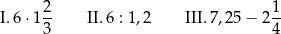
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczbami całkowitymi są wartości wyrażeń
A) I, II i III B) Tylko I i II C) Tylko II i III D) Tylko I i III
Asia wzięła udział w zajęciach teatralnych. Zajęcia składały się z 2 części. Każda część trwała tyle samo minut. Pomiędzy pierwszą a drugą częścią była 10–minutowa przerwa. Zajęcia rozpoczęły się o godzinie 17:45, a zakończyły o godzinie 19:05. Druga część zajęć rozpoczęła się o godzinie
A) 18:20 B) 18:25 C) 18:30 D) 18:35
Cenę laptopa obniżono najpierw o 15%, a później o 150 zł. Po obu obniżkach laptop kosztuje 2400 zł.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed tymi dwoma obniżkami laptop kosztował 3000 zł. | P | F |
| Po obu obniżkach cena laptopa stanowi 85% ceny początkowej. | P | F |
Wartość wyrażenia 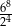 jest równa
jest równa
A) 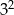 B)
B) 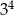 C)
C) 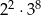 D)
D) 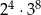
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 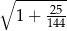 jest równa A/B .
jest równa A/B .
A) 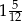 B)
B) 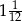
Wartość wyrażenia 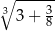 jest równa C/D .
jest równa C/D .
C) 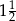 D)
D) 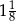
Na festyn przygotowano loterię, w której było 120 losów, w tym 80 wygrywających. Przed rozpoczęciem festynu dołożono jeszcze 20 losów wygrywających i 20 przegrywających. Czy prawdopodobieństwo wyciągnięcia losu wygrywającego w tej loterii zmieniło się po dołożeniu losów? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | różnica liczby losów wygrywających i przegrywających po dołożeniu losów jest taka sama jak na początku. |
| B) | dołożono tyle samo losów wygrywających co przegrywających. |
| C) | zmienił się stosunek liczby losów wygrywających do liczby wszystkich losów. |
Zależność między liczbą przekątnych (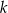 ) a liczbą boków (
) a liczbą boków ( ) wielokąta wypukłego określa wzór
) wielokąta wypukłego określa wzór 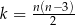 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba przekątnych w dwunastokącie wypukłym jest trzy razy większa od liczby przekątnych w czworokącie wypukłym. | P | F |
| Liczba przekątnych w ośmiokącie wypukłym jest o 11 większa od liczby przekątnych w sześciokącie wypukłym. | P | F |
W zeszycie w linie narysowano dwa równoległoboki i trójkąt w sposób pokazany na rysunku. Odległości między sąsiednimi liniami są jednakowe. Podstawy wszystkich tych figur mają taką samą długość. Pole równoległoboku 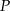 jest równe 4.
jest równe 4.
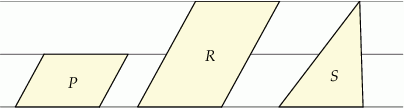
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole równoległoboku 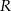 jest równe 8. jest równe 8. | P | F |
Pole trójkąta 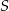 jest równe 4. jest równe 4. | P | F |
W trójkącie stosunek miar kątów jest równy 2 : 3 : 7.
Wybierz właściwą odpowiedź spośród podanych.
Trójkąt o podanych własnościach jest
A) rozwartokątny. B) prostokątny. C) ostrokątny. D) równoramienny.
Prostokąt 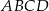 podzielono odcinkiem
podzielono odcinkiem 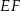 na dwa prostokąty. Odcinek
na dwa prostokąty. Odcinek 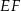 ma długość 11 cm, a odcinek
ma długość 11 cm, a odcinek 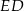 ma długość 2 cm. Pole prostokąta
ma długość 2 cm. Pole prostokąta 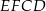 stanowi
stanowi  pola prostokąta
pola prostokąta 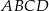 .
.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole prostokąta 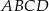 jest równe jest równe 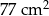 . . | P | F |
Odcinek 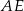 ma długość 7 cm. ma długość 7 cm. | P | F |
Bok rombu ma długość 17 cm, a jedna z jego przekątnych ma długość 30 cm. Pole tego rombu jest równe
A) 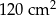 B)
B) 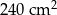 C)
C) 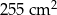 D)
D) 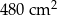
Dwa sześciany – jeden o krawędzi 2 i drugi o krawędzi 3 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 35 B) 47 C) 94 D) 142
Pewną kwotę rozdzielono na trzy nagrody pieniężne. Marcin dostał 2 razy więcej pieniędzy niż Jędrek, a Kamil 2 razy mniej niż Jędrek. Uzasadnij, że Kamil otrzymał 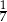 tej kwoty.
tej kwoty.
Na rysunku pokazano plan dwóch dróg, którymi Ula chodzi do szkoły.
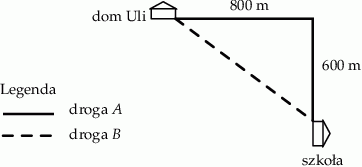
Przyjmij, że Ula porusza się ze stałą prędkością 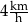 . Oblicz, o ile minut krócej Ula idzie do szkoły drogą
. Oblicz, o ile minut krócej Ula idzie do szkoły drogą 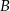 niż drogą
niż drogą 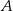 . Zapisz obliczenia.
. Zapisz obliczenia.
W kwiaciarni było trzy razy więcej czerwonych róż niż białych. Pan Nowak kupił 40 czerwonych róż i wtedy w kwiaciarni zostało dwa razy więcej białych róż niż czerwonych. Ile białych róż było w kwiaciarni?
Na rysunku przedstawiono kwadrat 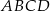 o polu
o polu 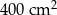 . Figurę tę podzielono na kwadrat
. Figurę tę podzielono na kwadrat 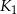 o polu
o polu 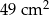 i kwadrat
i kwadrat 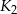 oraz figurę
oraz figurę 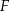 (patrz rysunek).
(patrz rysunek).
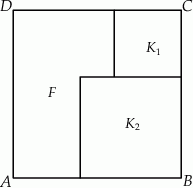
Oblicz obwód figury 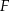 .
.

