/Szkoła podstawowa/Egzamin ósmoklasisty
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 13 maja 2023 Czas pracy: 100 minut
Wśród uczniów klas ósmych przeprowadzono ankietę – uczniowie odpowiadali na pytanie „Jaki jest twój ulubiony sport?”. Każdy uczeń podawał tylko jedną dyscyplinę sportu. Grę w tenisa wskazało 24 uczniów. Procentowy rozkład udzielonych odpowiedzi uczniów przedstawiono na poniższym diagramie.
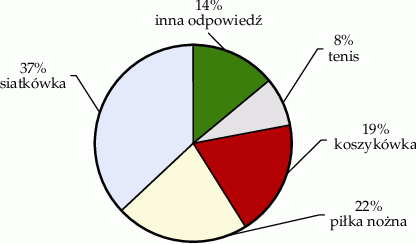
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Koszykówkę wybrało 57 uczniów. | P | F |
| Siatkówkę wybrało wybrało o 46 uczniów więcej niż uczniów, którzy wybrali piłkę nożną. | P | F |
Poniżej zapisano trzy liczby:
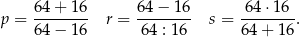
Który zapis przedstawia poprawnie uporządkowane liczby 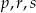 od największej do najmniejszej?
od największej do najmniejszej?
A) 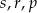 B)
B) 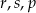 C)
C) 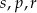 D)
D) 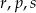
Spośród wszystkich liczb czterocyfrowych o sumie cyfr równej 12 wybrano liczbę największą i liczbę najmniejszą.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma wybranych liczb jest równa
A) 10329 B) 9339 C) 10519 D) 9419
Liczba 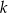 jest sumą liczb 243 i 162. Czy liczba
jest sumą liczb 243 i 162. Czy liczba 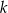 jest podzielna przez 81?
jest podzielna przez 81?
Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | suma cyfr liczby 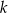 nie jest liczbą podzielną przez 81. nie jest liczbą podzielną przez 81. |
| B) | każda z liczb 243 i 162 dzieli się przez 81. |
| C) | suma cyfr liczby 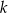 jest liczbą podzielną przez 81. jest liczbą podzielną przez 81. |
Dane są trzy liczby:
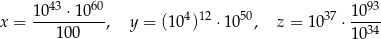
Która z tych liczb jest większa od liczby 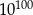 ?
?
A) Tylko  . B) Tylko
. B) Tylko  i
i 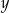 . C) Tylko
. C) Tylko 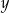 i
i  . D) Każda z liczb
. D) Każda z liczb 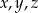 .
.
Do napełniania basenu służą dwa zawory. Jeżeli oba zawory są odkręcone jednocześnie, to basen napełnia się w ciągu 30 minut. Jeżeli odkręcony jest wyłącznie pierwszy zawór, to basen napełnia się w ciągu 66 minut. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Jeżeli odkręcony jest wyłącznie drugi zawór, to basen napełnia się w ciągu A/B minut.
A) 60 B) 55
Objętość wody, która przepłynie przez zawór pierwszy w ciągu 6 minut jest taka sama jak objętość wody, która przepłynie przez zawór drugi w ciągu C/D minut.
C) 4 D) 5
Dane są dwie liczby
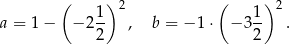
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia  jest równa A/B .
jest równa A/B .
A) 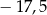 B) 18,5
B) 18,5
Wartość wyrażenia 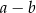 jest równa C/D .
jest równa C/D .
C) 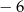 D) 7
D) 7
Dane są cztery liczby
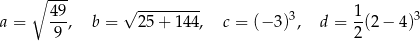
Które zdanie jest fałszywe?
A) Wśród liczb 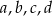 są dokładnie dwie liczby ujemne.
są dokładnie dwie liczby ujemne.
B) Liczba  jest większa niż liczba
jest większa niż liczba  .
.
C) Liczba 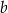 jest o 21 większa od liczby
jest o 21 większa od liczby 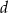 .
.
D) Liczba 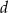 jest o 23 większa od liczby
jest o 23 większa od liczby  .
.
E) Wśród liczb 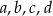 jest liczba, która nie jest liczbą całkowitą.
jest liczba, która nie jest liczbą całkowitą.
Dane są trzy liczby 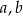 i
i  . Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Gdy 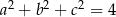 oraz
oraz  jest liczbą mniejszą od
jest liczbą mniejszą od 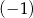 , to suma
, to suma 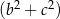 jest A/B .
jest A/B .
A) mniejsza od 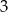 B) większa od
B) większa od 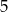
Gdy 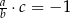 oraz
oraz 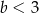 , to
, to 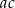 jest liczbą C/D .
jest liczbą C/D .
C) mniejszą od 3 D) większą od 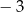
Długości boków trójkąta równoramiennego przedstawionego na rysunku opisano wyrażeniami algebraicznymi.
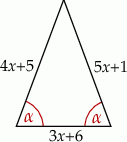
Obwód tego trójkąta jest równy
A) 42 B) 60 C) 48 D) 39
Na krótszym boku prostokąta zbudowano sześciokąt foremny o obwodzie 42 cm, a na dłuższym boku zbudowano pięciokąt foremny o obwodzie 55 cm. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole prostokąta jest równe 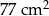 . . | P | F |
| Obwód prostokąta jest o 8 cm krótszy od obwodu sześciokąta foremnego zbudowanego na krótszym boku prostokąta. | P | F |
Dany jest trójkąt 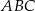 , w którym kąt
, w którym kąt 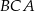 ma miarę
ma miarę 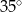 . Punkt
. Punkt 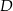 leży na boku
leży na boku 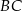 tego trójkąta. Odcinek
tego trójkąta. Odcinek 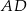 ma taką samą długość jak odcinek
ma taką samą długość jak odcinek 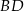 . Kąt
. Kąt 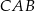 ma miarę
ma miarę 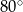 (zobacz rysunek poniżej).
(zobacz rysunek poniżej).
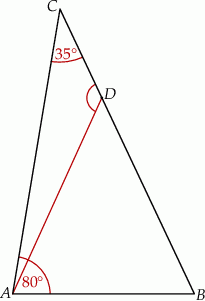
Kąt 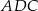 ma miarę
ma miarę
A) 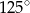 B)
B) 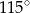 C)
C) 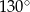 D)
D) 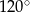
Suma długości wszystkich krawędzi ostrosłupa prawidłowego sześciokątnego jest równa 540. Krawędź boczna jest w tym ostrosłupie pięciokrotnie dłuższa od krawędzi podstawy.
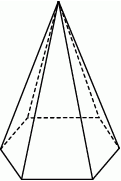
Długość krawędzi podstawy tego ostrosłupa jest równa
A) 15 B) 25 C) 50 D) 60
W pudełku było wyłącznie 216 kulek zielonych i 57 kulek niebieskich. Do tego pudełka dołożono pewną liczbę kulek niebieskich, a następnie usunięto tyle kulek zielonych, ile było kulek niebieskich w pudełku. Po tych zmianach prawdopodobieństwo wylosowania kulki niebieskiej jest równe 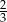 . Ile kulek zielonych usunięto z pudełka?
. Ile kulek zielonych usunięto z pudełka?
A) 87 B) 29 C) 144 D) 58
Trzech kolegów kupiło bilety autobusowe w tym samym automacie. Wiktor kupił 8 biletów 75–minutowych i zapłacił za te bilety 36 zł. Jacek kupił 6 biletów 20–minutowych i zapłacił za nie 15 zł. Przemek kupił 7 biletów 75–minutowych i 7 biletów 20–minutowych. Ile Przemek zapłacił za bilety?
A) 49 zł B) 51 zł C) 42 zł D) 56 zł
W jednej szklance o pojemności 250 mililitrów mieści się maksymalnie 90 gramów płatków owsianych, a w pojemniku o objętości 1,5 litra mieści się maksymalnie 1,05 kg rodzynek. Dziadek Kuby ma dwa takie same pojemniki. Pierwszy z tych pojemników jest całkowicie wypełniony płatkami owsianymi. Masa płatków owsianych przechowywanych w tym pojemniku jest równa 0,81 kg. Drugi pojemnik jest pusty. Czy w drugim pojemniku zmieściłoby się 1,5 kg rodzynek?
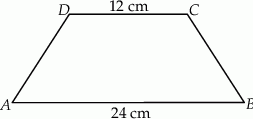
Podstawy trapezu równoramiennego 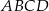 mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe
mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe 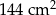 . Oblicz obwód trapezu
. Oblicz obwód trapezu 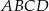 .
.
Pani Ewa odczytała na nawigacji samochodowej, że na pokonanie trasy długości 39 km potrzebuje 36 minut. Jaką prędkość jazdy wyrażoną w 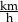 przyjęła nawigacja samochodowa w celu wyznaczenia czasu potrzebnego na pokonanie tej trasy?
przyjęła nawigacja samochodowa w celu wyznaczenia czasu potrzebnego na pokonanie tej trasy?
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
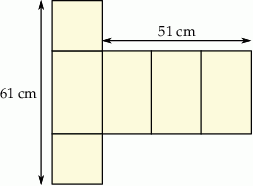
Oblicz objętość tego graniastosłupa.

