/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2019
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 6 kwietnia 2019 Czas pracy: 100 minut
Zuzia dojeżdża do szkoły autobusem linii 121. Droga z domu na przystanek zajmuje jej 7 minut, podróż autobusem trwa 14 minut, a czas dojścia do szkoły od przystanku zajmuje jej 12 minut. W tabeli zamieszczono fragment rozkładu jazdy autobusu linii 121, którym Zuzia dojeżdża do szkoły.
| Godzina | Minuty |
| 6 | 04 12 20 28 36 44 52 |
| 7 | 00 08 16 24 32 40 48 56 |
| 8 | 04 12 20 28 36 44 52 |
| 9 | 00 08 16 24 32 40 48 56 |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli Zuzia wyjdzie z domu o godz. 7:35, to będzie w szkole przed 8:15. | P | F |
| Jeżeli Zuzia dotarła do szkoły przed godz. 9:33, to wyszła z domu przed 8:55. | P | F |
Właściciel księgarni zaznaczył na diagramie informacje o dziennej sprzedaży trzech zbiorów zadań.
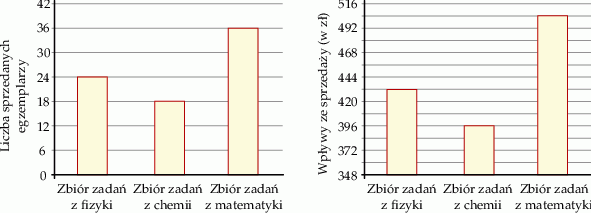
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Zbiór zadań z chemii jest droższy od pozostałych dwóch zbiorów zadań. | P | F |
| Średnia cena sprzedaży jednego zbioru zadań jest wyższa niż 20 zł | P | F |
Prosta 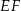 dzieli trapez równoramienny
dzieli trapez równoramienny 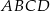 na romb
na romb 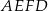 o obwodzie 52 cm i trapez
o obwodzie 52 cm i trapez 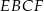 o obwodzie o 13 cm mniejszym od obwodu rombu
o obwodzie o 13 cm mniejszym od obwodu rombu 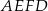 .
.
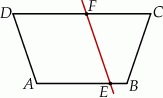
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma długości odcinków 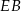 i
i 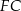 jest równa
jest równa
A) 14 cm B) 13 cm C) 15 cm D) 18 cm
Amelia i Jakub testują swoje elektryczne hulajnogi. W tym celu zmierzyli czasy przejazdu na trasie 600 m. Amelia pokonała tę trasę w czasie 180 s, a Jakub – w czasie 144 s.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Różnica średnich prędkości uzyskanych przez Jakuba i przez Amelię jest równa
A) 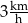 B)
B) 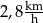 C)
C) 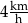 D)
D) 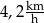
Liczba  jest największą liczbą dwucyfrową podzielną przez 2 i 3, a liczba
jest największą liczbą dwucyfrową podzielną przez 2 i 3, a liczba 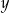 jest największą liczbą trzycyfrową o trzech różnych cyfrach parzystych. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest największą liczbą trzycyfrową o trzech różnych cyfrach parzystych. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Największy wspólny dzielnik liczb  i i 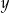 jest równy 96. jest równy 96. | P | F |
Najmniejsza wspólna wielokrotność liczb  i i 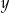 jest równa 864. jest równa 864. | P | F |
Informacja do zadań 6 i 7
Jeżeli 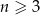 , to liczbę przekątnych wielokąta wypukłego o
, to liczbę przekątnych wielokąta wypukłego o  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru
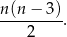
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wielokąt, który ma cztery razy więcej przekątnych niż boków ma A/B boków.
A) 10 B) 11
Liczba przekątnych wielokąta o 222 bokach jest liczbą C/D .
C) nieparzystą D) parzystą
Która z liczb nie jest liczbą przekątnych pewnego wielokąta wypukłego?
Wybierz odpowiedź spośród podanych.
A) 5 B) 9 C) 10 D) 14 E) 20
Punkty 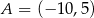 ,
, 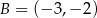 i
i 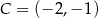 są kolejnymi wierzchołkami prostokąta
są kolejnymi wierzchołkami prostokąta 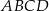 . Wierzchołek
. Wierzchołek 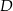 tego prostokąta ma współrzędne
tego prostokąta ma współrzędne
A) 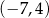 B)
B) 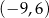 C)
C) 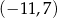 D)
D) 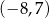
Dana jest liczba 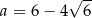 .
.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba o 2 mniejsza od połowy liczby  jest równa A/B .
jest równa A/B .
A) 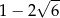 B)
B) 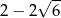
Połowa liczby o 2 większej od  równa C/D .
równa C/D .
C) 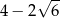 D)
D) 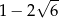
Iza rzuciła 10 razy standardową sześcienną kostką do gry. W trakcie rzutów obliczała sumę 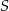 wyrzuconych oczek według następującej reguły: jeżeli liczba wyrzuconych oczek była nieparzysta, to dodawała tę liczbę do sumy
wyrzuconych oczek według następującej reguły: jeżeli liczba wyrzuconych oczek była nieparzysta, to dodawała tę liczbę do sumy 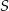 , a jeżeli liczba wyrzuconych oczek była parzysta, to odejmowała tę liczbę od
, a jeżeli liczba wyrzuconych oczek była parzysta, to odejmowała tę liczbę od 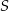 . Na diagramie przedstawiono wartości sumy
. Na diagramie przedstawiono wartości sumy 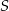 po kolejnych rzutach.
po kolejnych rzutach.
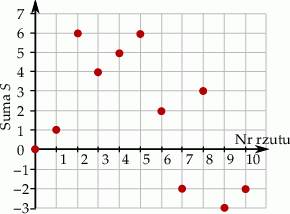
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Iza cztery razy wyrzuciła parzystą liczbę oczek. | P | F |
| Iza dwa razy wyrzuciła trzy oczka. | P | F |
Na rysunku przedstawiono sześcian  oraz trzy jego przekątne.
oraz trzy jego przekątne.
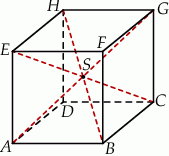
Czy kąty 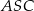 i
i 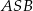 są równe? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
są równe? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | wszystkie przekątne sześcianu mają tę samą długość. |
| B) | trójkąty 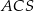 i i 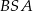 nie są przystające. nie są przystające. |
| C) | przekątne sześcianu są prostopadłe. |
W trójkącie 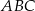 najmniejszą miarę ma kąt przy wierzchołku
najmniejszą miarę ma kąt przy wierzchołku 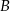 . Miara kąta przy wierzchołku
. Miara kąta przy wierzchołku 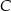 jest równa
jest równa 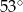 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 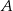 jest równa sumie miary kąta przy wierzchołku
jest równa sumie miary kąta przy wierzchołku 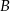 oraz miary kąta przy wierzchołku
oraz miary kąta przy wierzchołku 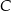 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt przy wierzchołku 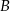 ma miarę ma miarę 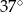 . . | P | F |
Trójkąt 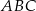 jest ostrokątny. jest ostrokątny. | P | F |
Tata Karola zainwestował w waluty elektroniczne i za 480 zł kupił bitmonety. Po pół roku sprzedał kupione bitmonety za 1 920 zł.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość bitmonet od momentu ich zakupu do momentu sprzedaży
A) wzrosła o 500%. B) wzrosła o 400%. C) wzrosła o 300%. D) wzrosła o 200%.
Z drewnianych listewek, które mają kształt prostopadłościanu o podstawie 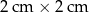 zbudowany drewniany szkielet przedstawiony na rysunku.
zbudowany drewniany szkielet przedstawiony na rysunku.
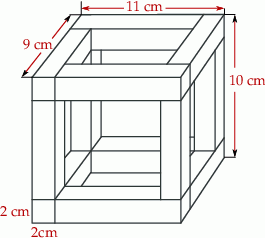
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Suma długości listewek, z których zbudowano szkielet jest równa A/B .
A) 120 cm B) 88 cm
Objętość drewna użytego do budowy szkieletu jest równa C/D .
C) 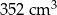 D)
D) 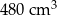
Prędkość średnia samochodu osobowego na odcinku autostrady długości 50 km wyniosła 120 km/h, a prędkość średnia motocyklisty na tym samym odcinku autostrady wyniosła 100 km/h. O ile minut więcej zajęło pokonanie tego odcinka autostrady motocykliście niż kierowcy samochodu osobowego? Wybierz odpowiedź spośród podanych.
A) 4 minuty B) 5 minut C) 6 minut D) 8 minut
Dwie przeciwległe ściany drewnianego sześcianu pomalowano na czerwono, a pozostałe – na biało. Ten sześcian rozcięto na 27 jednakowych sześcianów.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Sześć małych sześcianów ma dokładnie jedną ścianę pomalowaną farbą. | P | F |
| Tylko cztery małe sześciany mają jedną ścianę pomalowaną na biało. | P | F |
Równoległobok 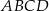 o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej
o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej  na dwa trapezy tak, jak pokazano na rysunku. Odcinek
na dwa trapezy tak, jak pokazano na rysunku. Odcinek 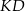 ma długość 4,8 cm.
ma długość 4,8 cm.
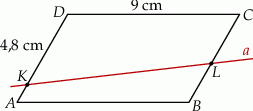
Pole trapezu 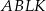 jest trzykrotnie mniejsze od pola równoległoboku
jest trzykrotnie mniejsze od pola równoległoboku 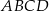 . Oblicz długość odcinka
. Oblicz długość odcinka 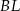 . Zapisz obliczenia.
. Zapisz obliczenia.
W każdym z dwóch pudełek znajduje się tyle samo kul. Kule te są w jednym z dwóch kolorów: czarne lub białe. Prawdopodobieństwo wylosowania kuli białej z pierwszego pudełka jest równe 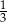 i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?
i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?
Grupa 29 osób chce się podzielić na kilka grup pięcio i trzyosobowych. Ile grup trzyosobowych może powstać w ten sposób? Podaj wszystkie możliwości.
Objętość prostopadłościennego basenu o szerokości 6 m i długości 10 m jest równa 120 000 litrów. Ile litrów farby potrzeba do pomalowania dna i ścian basenu, jeżeli jeden litr farby wystarcza do pomalowania 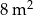 powierzchni?
powierzchni?
W maratonie czytelniczym rywalizowało troje uczniów: Kasia, Ela i Romek. Kasia przeczytała 11 książek, co stanowiło 44% wszystkich książek przeczytanych przez te 3 osoby. Romek przeczytał o 4 książki mniej od Eli. Oblicz, ile książek przeczytał Romek, a ile – Ela.
Objętość ostrosłupa prawidłowego czworokątnego jest równa 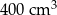 , a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
, a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.

