/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2019
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 16 marca 2019 Czas pracy: 100 minut
Firma transportowa Paka korzysta z samochodów dostawczych, które mogą przewozić towar o maksymalnej masie 1,2 tony. Maksymalne wymiary jednej prostopadłościennej przesyłki, która może zostać przewieziona takim samochodem wynoszą 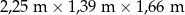 . W tabeli zapisano wymiary i masę jednej paczki oraz liczbę paczek w sześciu zamówieniach transportowych
. W tabeli zapisano wymiary i masę jednej paczki oraz liczbę paczek w sześciu zamówieniach transportowych
| Nr zamówienia | Liczba paczek | Wymiary | Masa |
| 1 | 1 | 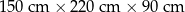 | 1199 kg |
| 2 | 3 | 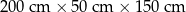 | 400 kg |
| 3 | 8 | 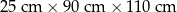 | 120 kg |
| 4 | 2 | 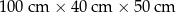 | 620 kg |
| 5 | 5 | 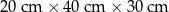 | 250 kg |
| 6 | 4 | 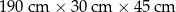 | 290 kg |
Ile sposród tych zamówień może zostać zrealizowanych jednym samochodem dostawczym? Wybierz właściwą odpowiedź spośród podanych.
A) 2 B) 3 C) 4 D) 5 E) 6
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 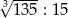 jest równa wartości wyrażenia A/B .
jest równa wartości wyrażenia A/B .
A) 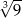 B)
B) 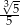
Wartość wyrażenia 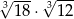 jest równa wartości wyrażenia C/D .
jest równa wartości wyrażenia C/D .
C) 6 D) 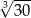
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| 40% liczby 140 to tyle samo, co 140% liczby 40. | P | F |
| 30% liczby 42 to tyle samo, co 60% liczby 84. | P | F |
W magazynie znajdują się: 264 stoły i 1836 krzeseł. Meble te podzielono na  grup w ten sposób, że w każdej grupie jest tyle samo krzeseł i w każdej grupie jest tyle samo stołów. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
grup w ten sposób, że w każdej grupie jest tyle samo krzeseł i w każdej grupie jest tyle samo stołów. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba  może być równa 8. może być równa 8. | P | F |
Największa możliwa wartość liczby  to 12. to 12. | P | F |
Z okazji Międzynarodowego Dnia Liczby 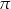 zorganizowano konkurs matematyczny w jednej ze szkół podstawowych. Każdy z uczestników konkursu zajmował jedno z miejsc numerowanych kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło konkurs na danym miejscu. Wiadomo, że 49% uczniów zajęło miejsce o numerze wyższym niż Amelia.
zorganizowano konkurs matematyczny w jednej ze szkół podstawowych. Każdy z uczestników konkursu zajmował jedno z miejsc numerowanych kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło konkurs na danym miejscu. Wiadomo, że 49% uczniów zajęło miejsce o numerze wyższym niż Amelia.
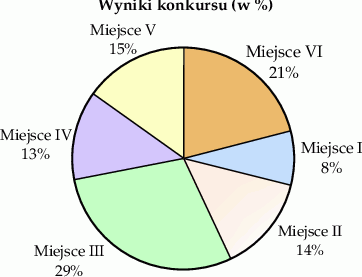
Ile procent uczniów zakończyło konkurs na miejscach o numerach niższych niż Amelia? Wybierz właściwą odpowiedź spośród podanych.
A) 8% B) 22% C) 51% D) 36%
Prostokąt o wymiarach 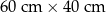 przecięto na dwa takie same prostokąty (patrz rysunek I). Następnie jeden z tych prostokątów obrócono o
przecięto na dwa takie same prostokąty (patrz rysunek I). Następnie jeden z tych prostokątów obrócono o 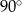 i ułożono na drugim (patrz rysunek II).
i ułożono na drugim (patrz rysunek II).
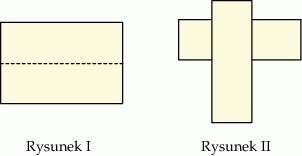
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Figura z rysunku II ma pole 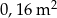 | P | F |
| Figura z rysunku II ma obwód równy 2,4 m. | P | F |
Narysowany kwadrat należy wypełnić tak, aby iloczyny liczb w każdym wierszu, każdej kolumnie i na obu przekątnych kwadratu były takie same.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn wszystkich liczb w kwadracie jest równy 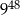 . . | P | F |
W zacieniowane pole kwadratu należy wpisać liczbę 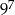 . . | P | F |
Tomek poprawnie zaokrąglił liczbę 5985 do pełnych setek i otrzymał liczbę  , a Ania poprawnie zaokrągliła liczbę 6489 do pełnych tysięcy i otrzymała liczbę
, a Ania poprawnie zaokrągliła liczbę 6489 do pełnych tysięcy i otrzymała liczbę 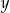 .
.
Czy liczby  i
i 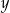 są równe? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.
są równe? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | początkowa liczba Tomka jest mniejsza od początkowej liczby Ani. |
| B) | liczba Tomka jest większa od 5950, a liczba Ani jest mniejsza od 6500. |
| C) | otrzymane zaokrąglenia różnią się o 100. |
Na bokach trójkąta prostokątnego 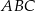 zaznaczono punkty
zaznaczono punkty 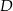 i
i 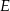 . Odcinek
. Odcinek 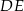 podzielił trójkąt
podzielił trójkąt 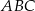 na dwa wielokąty: trójkąt prostokątny
na dwa wielokąty: trójkąt prostokątny 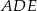 i czworokąt
i czworokąt 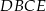 , jak na rysunku. Odcinek
, jak na rysunku. Odcinek 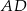 ma długość
ma długość 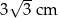 , a odcinek
, a odcinek 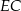 ma długość 2 cm.
ma długość 2 cm.
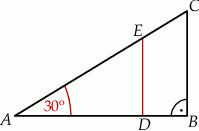
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość odcinka 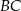 jest równa
jest równa
A) 6 cm B) 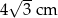 C) 2 cm D) 4 cm E)
C) 2 cm D) 4 cm E) 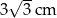
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Średnia arytmetyczna zestawu liczb: 12, 5, 13, 9, 2, 7 zwiększy się o 75%, gdy w miejsce 2 wpiszemy liczbę
A) 36 B) 84 C) 38 D) 14
O liczbie  wiemy, że
wiemy, że 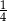 tej liczby jest o
tej liczby jest o  mniejsza od
mniejsza od 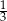 tej liczby. Które równanie pozwoli wyznaczyć liczbę
tej liczby. Które równanie pozwoli wyznaczyć liczbę  ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) 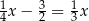 B)
B) 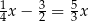 C)
C) 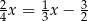 D)
D) 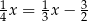
Przekątne trapezu 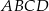 przedstawionego na rysunku przecinają się w punkcie
przedstawionego na rysunku przecinają się w punkcie 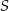 .
.
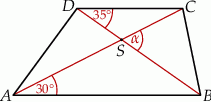
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 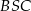 ma miarę ma miarę 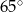 . . | P | F |
Trójkąty 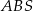 i i 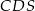 mają równe kąty. mają równe kąty. | P | F |
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki prostokąta 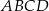 :
: 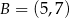 ,
, 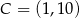 ,
, 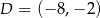 .
.
Jakie współrzędne ma punkt A? Wybierz właściwą odpowiedź spośród podanych.
A) 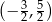 B)
B) 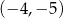 C)
C) 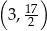 D)
D) 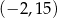
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba 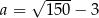 jest A/B .
jest A/B .
A) mniejsza od 10 B) większa od 10
Liczba 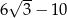 jest C/D .
jest C/D .
C) ujemna D) dodatnia
Na rysunkach przedstawiono graniastosłup prawidłowy i ostrosłup prawidłowy. Wszystkie krawędzie obu brył są jednakowej długości.
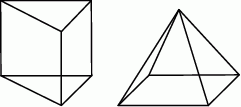
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Suma długości wszystkich krawędzi graniastosłupa jest większa niż suma długości wszystkich krawędzi ostrosłupa. | P | F |
| Całkowite pole powierzchni graniastosłupa jest większe niż całkowite pole powierzchni ostrosłupa. | P | F |
Zdarzenie losowe polega na wybraniu jednej krawędzi ustalonego wcześniej graniastosłupa prostego. Oblicz jakie jest prawdopodobieństwo, że wybrana krawędź jest krawędzią boczną tego graniastosłupa.
Wykaż, że jeżeli w pewnym roku pierwszy dzień kalendarzowego lata (21 czerwca) wypada w niedzielę, to pierwszy dzień kalendarzowej zimy (21 grudnia) wypada w poniedziałek.
Karol przykleja na kartce formatu A4 (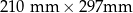 ) kwadraty o boku 2 cm, według wzoru, którego fragment pokazano na rysunku.
) kwadraty o boku 2 cm, według wzoru, którego fragment pokazano na rysunku.
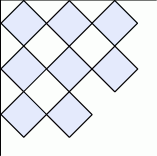
Przekątne każdego kwadratu są równoległe do krawędzi kartki i kwadraty stykają się jednym wierzchołkiem. Oblicz ile maksymalnie takich kwadratów Karol będzie mógł przykleić na kartce. Do obliczeń przyjmij przybliżenie 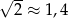 .
.
Na rysunku przedstawiono dwie różne ściany ostrosłupa prawidłowego czworokątnego. Jedna jest kwadratem o boku 10 cm, a druga – trójkątem równoramiennym o podstawie 10 cm i ramieniu 13 cm.
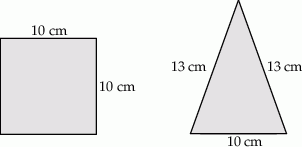
Oblicz pole powierzchni całkowitej ostrosłupa o takich wymiarach.
Cena godziny korzystania z basenu wynosi 12 zł. Można jednak kupić miesięczną kartę rabatową za 49 złotych, upoważniającą do obniżki cen, i wtedy za pierwsze 10 godzin pływania płaci się 8 złotych za godzinę, a za każdą następną godzinę – 9 złotych. Kamila kupiła kartę rabatową, a Kacper zdecydował się korzystać z basenu bez karty rabatowej. Po miesiącu korzystania z basenu, okazało się, że Kamila i Kacper byli na basenie przez dokładnie tyle samo godzin, oraz ich wydatki na basen były dokładnie takie same. Ile godzin spędziła na basenie Kamila?
Pan Kamil wyjechał o godzinie 9:00 w podróż samochodową z Torunia do Warszawy. Wykres przedstawia jego odległość od Torunia w zależności od czasu jazdy.
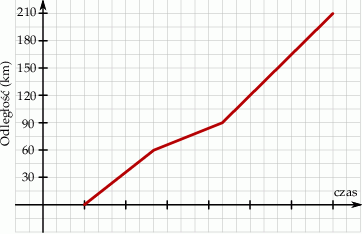
Średnia prędkość z jaką pokonał ten dystans jest równa 70 km/h. Oblicz z jaką największą prędkością poruszał się Pan Kamil w trakcie swojej podróży do Warszawy.

