Zadanie nr 1485999
W urnie znajdują się 52 kule, które mogą się różnić wyłącznie kolorem. Wśród nich jest 26 kul białych, 6 kul czarnych, 12 niebieskich i 8 zielonych. Z tej urny losujemy czterokrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania czterech kul, wśród których są 2 białe i 2 niebieskie. Wynik podaj w postaci ułamka nieskracalnego.
Rozwiązanie
W sumie z urny losujemy cztery kule, więc jest
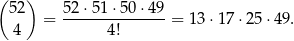
zdarzeń elementarnych. Zdarzeń sprzyjających jest
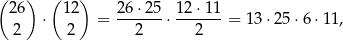
więc interesujące nas prawdopodobieństwo jest równe
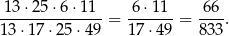
Odpowiedź: