/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna

Zadanie nr 1841352

W urnie znajduje się dwa razy więcej kul białych niż czarnych. Losujemy z urny jednocześnie dwie kule. Prawdopodobieństwo wylosowania obu kul białych jest równe 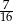176 . Oblicz prawdopodobieństwo wylosowania kul różnych kolorów.

Wersja PDF

Rozwiązanie

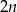Oznaczmy liczbę kul czarnych przez n . W takim razie jest 2n kul białych. Za zdarzenia elementarne przyjmujemy dwuelementowe zbiory wylosowanych kul, czyli

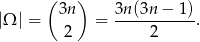
( ) 3n 3n-(3n−--1) |Ω | = 2 = 2 .

Dwie kule białe możemy wybrać na

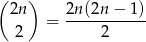
( ) 2n 2n-(2n−--1) 2 = 2

sposoby. W takim razie podane prawdopodobieństwo prowadzi do równania

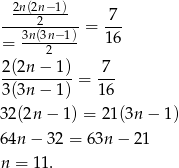
2n(2n−1) -----2-----= -7- = 3n(3n−-1)- 16 2 2(2n-−-1)- -7- 3(3n − 1) = 16 32(2n − 1) = 21(3n − 1) 64n − 32 = 63n − 21 n = 11 .

Dwie kule w różnych kolorach możemy wybrać na

11 ⋅22

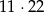
sposoby (wybieramy jedną kulę białą i jedną kulę czarną), więc interesujące nas prawdopodobieństwo jest równe

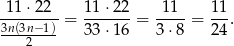
11 ⋅22 11⋅ 22 11 11 -------- = -------= ---- = ---. 3n(3n2−1) 33⋅ 16 3 ⋅8 24

 
Odpowiedź: 11 24

Wersja PDF