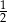Zadanie nr 2180606
W urnie znajduje się 5 kul białych i 3 czarne. Wyjmujemy losowo 4 kule. Oblicz prawdopodobieństwo, że wśród wyjętych są przynajmniej 2 kule czarne.
Rozwiązanie
W urnie jest 8 kul, więc
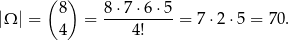
Jeżeli mają być co najmniej 2 kule czarne, to są dwie lub trzy.
Jeżeli są trzy kule czarne, to białą można do nich dobrać na 5 sposobów. Jest więc 5 takich zdarzeń.
Dwie kule czarne możemy wybrać na
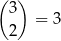
sposoby. Do tego dobieramy dwie kule białe. Można to zrobić na
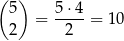
sposobów. Razem jest więc 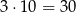 takich zdarzeń.
takich zdarzeń.
Prawdopodobieństwo wynosi więc
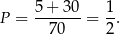
Odpowiedź: