/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna

Zadanie nr 2426437

Z urny zawierającej 7 kul białych i 3 kule czarne wylosowano bez zwracania 4 kule. Jakie jest prawdopodobieństwo tego, że stosunek liczby kul czarnych do liczby kul białych w urnie uległ zwiększeniu?

Wersja PDF

Rozwiązanie

Wszystkich możliwych wyników losowania jest

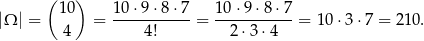
( 10) 10 ⋅9 ⋅8 ⋅7 1 0⋅9 ⋅8 ⋅7 |Ω | = = ----------- = ----------- = 1 0⋅3 ⋅7 = 2 10. 4 4! 2 ⋅3 ⋅4

Na początku stosunek liczby kul czarnych do białych wynosi 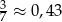3 ≈ 0,43 7 . Aby stosunek ten uległ zwiększeniu musimy wylosować co najmniej 3 kule białe (bo przy wylosowanych 2 kulach białych interesujący nas stosunek będzie równy: 15 = 0,2 ).

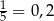Obliczmy ile jest takich zdarzeń. Cztery kule białe możemy wylosować na

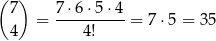
( ) 7 7⋅-6⋅5-⋅4- 4 = 4! = 7⋅5 = 35

sposobów. Trzy kule białe i jedną czarną możemy wylosować na

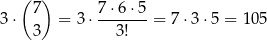
( ) 7 7 ⋅6⋅ 5 3⋅ = 3 ⋅------- = 7 ⋅3⋅ 5 = 105 3 3 !

sposobów. Interesujące nas prawdopodobieństwo jest więc równe

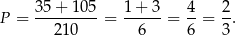
35+ 105 1+ 3 4 2 P = ---------= ------= --= --. 210 6 6 3

 
Odpowiedź: 2 3

Wersja PDF