/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna

Zadanie nr 2909782

Ile maksymalnie kul zielonych można włożyć do urny, w której jest 7 kul czerwonych, aby prawdopodobieństwo wylosowania 2 kul różnokolorowych było większe lub równe 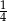14 ?

Wersja PDF

Rozwiązanie

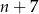Powiedzmy, że wkładamy n kul. W takim razie dwie kule wybieramy ze zbioru n + 7 kul, czyli

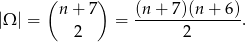
( ) |Ω | = n + 7 = (n+--7)(n-+-6). 2 2

Dwie kule różnokolorowe możemy wybrać na

n ⋅7

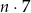
sposobów (wybieramy jedną zieloną i jedną czerwoną) i prawdopodobieństwo wynosi

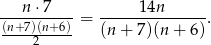
---n⋅-7---= ------14n------. (n+7)(n+-6) (n + 7 )(n + 6) 2

Pozostało rozwiązać nierówność

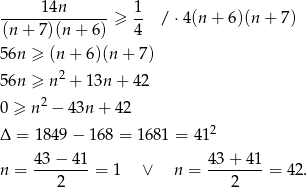
14n 1 ---------------≥ -- / ⋅4(n + 6)(n + 7) (n + 7)(n + 6 ) 4 56n ≥ (n+ 6)(n + 7) 2 56n ≥ n + 13n + 42 0 ≥ n2 − 43n + 42 Δ = 1849 − 168 = 1681 = 4 12 43− 41 4 3+ 4 1 n = --------= 1 ∨ n = -------- = 42. 2 2

Zatem maksymalnie możemy włożyć 42 kule zielone.  
Odpowiedź: 42

Wersja PDF