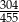Zadanie nr 3518289
Liczby kul białych, niebieskich i czerwonych tworzą - w podanej kolejności - ciąg arytmetyczny o różnicy 2. Spośród tych kul losujemy jednocześnie trzy. Prawdopodobieństwo wylosowania trzech kul, z których każda jest innego koloru wynosi 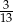 . Oblicz prawdopodobieństwo wylosowania z tej urny trzech kul, wśród których dwie są tego samego koloru, jeśli wiadomo, że liczba wszystkich kul w urnie jest nieparzysta.
. Oblicz prawdopodobieństwo wylosowania z tej urny trzech kul, wśród których dwie są tego samego koloru, jeśli wiadomo, że liczba wszystkich kul w urnie jest nieparzysta.
Rozwiązanie
Z podanych informacji wiemy, że liczby kul białych, niebieskich i czerwonych są równe, 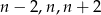 . Ponadto suma
. Ponadto suma 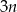 tych liczb ma być nieparzysta, czyli
tych liczb ma być nieparzysta, czyli  jest nieparzyste. Trzy kule z urny możemy wybrać na
jest nieparzyste. Trzy kule z urny możemy wybrać na
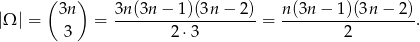
Zdarzeń, w których każda kula ma inny kolor jest
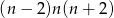
(wybieramy po jednej kuli każdego koloru). Mamy zatem równanie
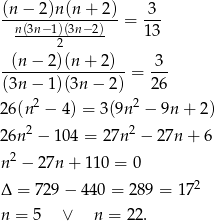
Ponieważ  ma być nieparzyste,
ma być nieparzyste, 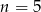 i
i
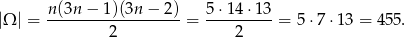
Policzmy teraz ile jest zdarzeń z dwoma kulami tego samego koloru. Przypomnijmy, że kul mamy odpowiednio 3,5,7. Mamy więc
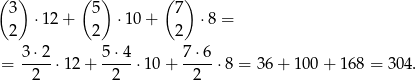
zdarzeń sprzyjających. Zatem prawdopodobieństwo wynosi
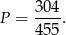
Odpowiedź: