Zadanie nr 4123113

W każdej z czterech urn są 24 kule, w tym dokładnie 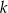białych. Z każdej urny losujemy jedną kulę. Dla jakiej wartości 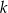prawdopodobieństwo wylosowania dokładnie dwóch kul białych jest największe? Oblicz to największe prawdopodobieństwo.

Rozwiązanie

Jest

4 |Ω | = 24

zdarzeń elementarnych – z każdej z 4 urn losujemy jedną z 24 kul.

Zdarzeń sprzyjających jest

( ) 4 ⋅k2 ⋅ (2 4− k)2 = 4-⋅3 ⋅k2(24− k)2 = 6k2(24 − k)2 2 2

(wybieramy dwie urny z białymi kulami, potem z każdej z tych dwóch urn wybieramy jedną z kul białych, a na koniec z każdej z dwóch pozostałych urn wybieramy kulę, która nie jest biała). Interesujące nas prawdopodobieństwo jest więc równe

2 2 6k-(24−--k)-. 244

Wystarczy teraz ustalić jaka jest największa możliwa wartość wyrażenia

2 2 2 2 2 3 4 f (k) = k (24 − k) = k (576 − 48k + k ) = 576k − 48k + k .

Żeby móc korzystać z pochodnej, traktujemy to wyrażenie jak funkcję o dziedzinie k ∈ ⟨0 ,2 4⟩ . Liczymy pochodną

f′(k) = 1152k − 1 44k2 + 4k3 = 4k(k2 − 36k + 288 ).

Rozkładamy jeszcze trójmian w nawiasie

Δ = 362 − 4 ⋅288 = 1296 − 1152 = 144 = 12 2 3 6− 1 2 36 + 12 k = -------- = 12 lub k = --------= 24. 2 2

Pochodna jest więc równa

′ f (k) = 4k(k − 12)(k − 24)

Widać teraz, że pochodna jest dodatnia w przedziale (0,12) i ujemna w przedziale (12,24 ) . To oznacza, że funkcja rośnie w przedziale (0,12 ⟩ i maleje w przedziale ⟨1 2,24) . W takim razie interesujące nas prawdopodobieństwo jest największe dla k = 12 . Jest ono wtedy równe