/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna

Zadanie nr 5138852

Dodaj do ulubionych
Dodaj do rozwiązanych

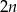W urnie znajduje się n kul czarnych i 2n kul białych (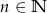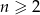n ∈ N , n ≥ 2 ). Losujemy jednocześnie dwie kule. Dla jakich n prawdopodobieństwo wylosowania dwóch kul tego samego koloru jest większe od prawdopodobieństwa wylosowania dwóch kul różnych kolorów?

Rozwiązanie

Przyjmijmy, że zdarzenia elementarane to nieuporządkowane pary wylosowanych kul. Zatem

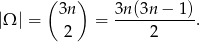
( ) |Ω | = 3n = 3n-(3n−--1). 2 2

Tak naprawdę, powyższy rachunek nie będzie nam potrzebny, bo mamy tylko porównywać prawdopodobieństwa, a one oba mają ten sam mianownik.

Możliwości wylosowania dwóch kul tego samego koloru jest

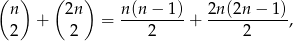
( ) ( ) n 2n n(n − 1) 2n(2n − 1) + = ---------+ -----------, 2 2 2 2

(obie są czarne lub obie są białe), a możliwości wylosowania dwóch kul w różnych kolorach jest

n ⋅2n

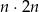
(jedna jest czarna, druga biała). Mamy zatem nierówność

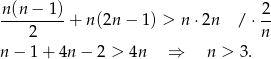
n(n − 1) 2 ---------+ n(2n − 1) > n ⋅2n / ⋅-- 2 n n − 1 + 4n − 2 > 4n ⇒ n > 3.

 
Odpowiedź: n > 3

Wersja PDF