Zadanie nr 5854230
W urnie są 3 kule białe, 4 czarne i 5 zielonych. Losujemy ze zwracaniem 3 kule. Oblicz prawdopodobieństwo tego, że wśród wylosowanych kul będą kule biała i czarna.
Rozwiązanie
Jeżeli za zdarzenia elementarne przyjmiemy uporządkowane trójki wylosowanych kul, to mamy
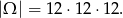
Spróbujmy teraz dokładnie policzyć ilość zdarzeń sprzyjających.
Sposób I
Jeżeli pierwsza z wylosowanych kul jest zielona, to pozostałe dwie muszą być białą i czarną. Takich zdarzeń mamy
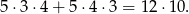
Jeżeli pierwsza z wylosowanych kul jest biała, to wśród pozostałych dwóch musi być czarna. Licząc osobno zdarzenia z kulą czarną i zieloną, czarną i białą i z dwoma czarnymi takich zdarzeń jest
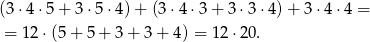
Jeżeli pierwsza z wylosowanych kul jest czarna, to wśród pozostałych dwóch musi być biała. Licząc osobno zdarzenia z kulą białą i zieloną, białą i czarną i z dwoma białymi takich zdarzeń jest
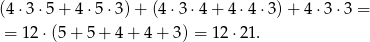
Zatem prawdopodobieństwo wynosi
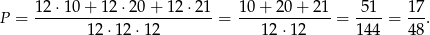
Sposób II
Przyjmijmy taką samą przestrzeń zdarzeń elementarnych, ale tym razem policzmy prawdopodobieństwo zdarzenia przeciwnego, tzn. policzmy ile jest takich zdarzeń, w których nie ma kuli białej lub czarnej. Zdarzeń bez kuli białej jest
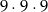
a zdarzeń bez kuli czarnej jest
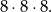
Jest w tym jednak mały haczyk, bo zdarzenia składające się z samych kul zielonych policzyliśmy podwójnie, musimy je więc odjąć. Jest ich
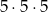
Zatem prawdopodobieństwo zdarzenia przeciwnego wynosi
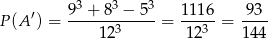
Zatem
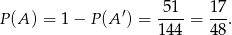
Odpowiedź: