Zadanie nr 5915287
Z urny, w której jest 5 kul czerwonych i 7 czarnych wyjęto dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wyjęto kule w różnych kolorach.
Rozwiązanie
Łączni w urnie mamy 12 kul i wyciągamy spośród nich 2 kule bez zwracania, więc możemy to zrobić na
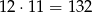
sposoby. Żeby kule były w różnych kolorach to jedna musi być czerwona, a druga czarna. Musimy jednak pamiętać, że możemy wylosować najpierw czarną, a później czerwoną albo najpierw czerwoną, a później czarną. Zatem zdarzeń sprzyjających jest
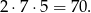
Zatem prawdopodobieństwo wynosi
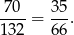
Odpowiedź: