/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna

Zadanie nr 7597228

Z pojemnika, w którym znajduje się pięć kul: dwie białe i trzy czerwone, losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę białą. Wynik przedstaw w postaci ułamka nieskracalnego.

Wersja PDF

Rozwiązanie

Sposób I

Parę kul możemy wybrać na

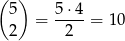
( 5) 5 ⋅4 = ---- = 1 0 2 2

sposobów. Jeżeli chcemy otrzymać co najmniej jedną kulę białą, to albo obie są białe – jest jedna taka sytuacja, albo jedna jest biała, a druga czerwona – takich sytuacji jest

2⋅3 = 6.

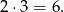
Interesujące nas prawdopodobieństwo jest więc równe

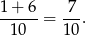
1-+-6-= 7-. 10 10

Sposób II

Tym razem za zdarzenia sprzyjające przyjmijmy pary 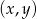(x ,y) wylosowanych kul. Pierwszą kulę możemy wybrać na 5 sposobów, a drugą na 4 sposoby, więc jest

5 ⋅4 = 20

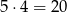
takich par. Wypisujemy teraz zdarzenia sprzyjające

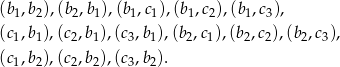
(b1,b2),(b2,b1),(b 1,c1),(b1,c2),(b1,c3), (c1,b1),(c2,b1),(c3,b1),(b2,c1),(b2,c2),(b2,c3), (c ,b ),(c ,b ),(c ,b ). 1 2 2 2 3 2

Jak widać jest 14 zdarzeń sprzyjających, więc interesujące nas prawdopodobieństwo jest równe

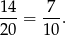
14-= -7-. 20 1 0

Sposób III

Rysujemy drzewko opisujące przebieg losowania

PIC

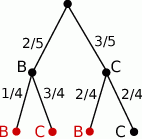
Z drzewka odczytujemy interesujące nas prawdopodobieństwo

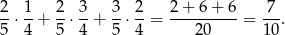
2 1 2 3 3 2 2+ 6+ 6 7 -⋅ --+ --⋅--+ --⋅--= ----------= ---. 5 4 5 4 5 4 20 1 0

 
Odpowiedź: -7 10

Wersja PDF