/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna

Zadanie nr 8061085

W urnie znajdują się kule białe, zielone i czerwone. Kul zielonych jest dwa razy więcej niż kul białych, a kul czerwonych jest 3 razy więcej niż białych. Wyjęto dwa razy po jednej kuli bez zwracania. Oblicz liczbę kul białych w urnie, jeśli prawdopodobieństwo wylosowania dwóch kul zielonych jest równe 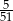-5 51 .

Wersja PDF

Rozwiązanie

Oznaczmy przez 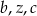b,z,c odpowiednio liczbę białych, zielonych i czerwonych kul. Wówczas z założeń mamy

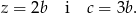
z = 2b i c = 3b.

Zatem wszystkich kul jest

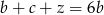
b+ c+ z = 6b

i mamy

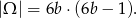
|Ω | = 6b ⋅(6b− 1).

możliwości wybrania pary kul z urny (uwzględniamy kolejność).

Dwie kule zielone możemy wybrać na

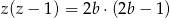
z(z − 1) = 2b⋅(2b − 1 )

sposobów, co daje nam równanie

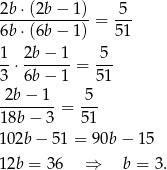
2b⋅ (2b− 1) 5 -------------= --- 6b⋅ (6b− 1) 51 1- 2b-−-1- 5-- 3 ⋅ 6b − 1 = 51 2b-−-1--= 5-- 18b − 3 51 1 02b− 51 = 90b − 1 5 1 2b = 36 ⇒ b = 3.

 
Odpowiedź: W urnie są 3 kule białe

Wersja PDF