/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna

Zadanie nr 8270845

Z urny, w której znajduje się 20 kul białych i 2 czarne losujemy n kul. Znajdź najmniejszą wartość n , taką przy której prawdopodobieństwo wylosowania przynajmniej jednej kuli czarnej jest większe od 12 .

Wersja PDF

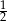Rozwiązanie

Łatwiejsze do policzenia jest zdarzenie przeciwne: 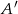′ A – wszystkie wylosowane kule są białe. Musimy sprawdzić, kiedy prawdopodobieństwo tego zdarzenia jest nie większe niż 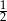12 . Liczymy

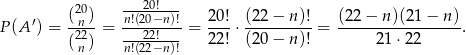
(20) n!(2200!−n)! 20! (22− n)! (22 − n )(21− n) P (A′) = -2n2- = ---22!----= ---⋅ ---------= -----------------. ( n) n!(22−n)! 22! (20− n)! 21⋅2 2

Mamy zatem nierówność

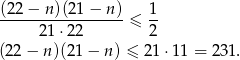
(22− n)(21 − n) 1 -----------------≤ -- 21 ⋅22 2 (22 − n )(21− n) ≤ 21 ⋅11 = 231.

Najmniejsze rozwiązanie tej nierówności najłatwiej jest zgadnąć wstawiając kolejne wartosci n , Ponieważ

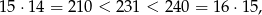
15 ⋅14 = 2 10 < 231 < 240 = 16 ⋅15,

najmniejszą wartością jest 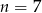n = 7 .  
Odpowiedź: n = 7

Wersja PDF