Zadanie nr 9178105
Co czwarta kula w urnie to biała, pozostałe mają kolor czarny lub niebieski. Losujemy jedna kulę. Prawdopodobieństwo wylosowania kuli niebieskiej lub białej jest dwukrotnie mniejsze niż prawdopodobieństwo wylosowania kuli niebieskiej lub czarnej. Oblicz prawdopodobieństwo wylosowania kuli czarnej.
Rozwiązanie
Oznaczmy przez 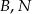 i
i 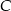 prawdopodobieństwa wylosowania kuli białej, niebieskiej i czarnej odpowiednio. Z podanych danych wiemy, że
prawdopodobieństwa wylosowania kuli białej, niebieskiej i czarnej odpowiednio. Z podanych danych wiemy, że
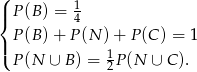
Druga równość wynika z tego, że w urnie nie ma innych kul niż białe, niebieskie i czarne. Ponadto
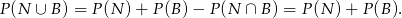
Podobnie
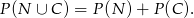
O równościach tego typu najlepiej jest sobie mysleć w kategoriach zdarzeń sprzyjających: 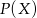 - mierzy ilość zdarzeń sprzyjających
- mierzy ilość zdarzeń sprzyjających 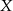 , zatem
, zatem 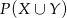 i
i 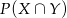 mierzą ilość darzeń sprzyającym
mierzą ilość darzeń sprzyającym 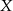 lub
lub 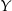 oraz
oraz 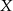 i
i 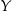 odpowiednio.
odpowiednio.
Mamy zatem układ równań
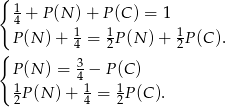
Otrzymujemy stąd
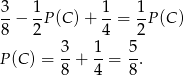
Odpowiedź: 

