Zadanie nr 9219208
Z urny zawierającej 10 kul ponumerowanych kolejnymi liczbami od 1 do 10 losujemy jednocześnie trzy kule. Oblicz prawdopodobieństwo zdarzenia 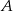 polegającego na tym, że numer jednej z wylosowanych kul jest równy sumie numerów dwóch pozostałych kul.
polegającego na tym, że numer jednej z wylosowanych kul jest równy sumie numerów dwóch pozostałych kul.
Rozwiązanie
Za zdarzenia elementarne przyjmujemy trójelementowe zbiory otrzymanych liczb, więc
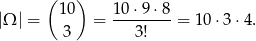
Sposób I
Wypisujemy wszystkie zdarzenia sprzyjające.
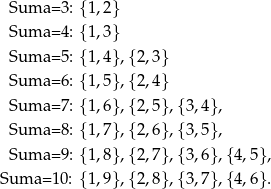
Jest więc
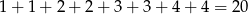
zdarzeń sprzyjających i prawdopodobieństwo jest równe
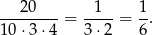
Sposób II
Powiedzmy, że 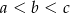 są trzema liczbami spełniającymi warunki zadania, tzn.
są trzema liczbami spełniającymi warunki zadania, tzn. 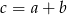 . Zauważmy, że po wybraniu
. Zauważmy, że po wybraniu  i
i 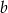 dla
dla  nie ma żadnego wyboru, więc wystarczy policzyć na ile sposobów możemy wybrać
nie ma żadnego wyboru, więc wystarczy policzyć na ile sposobów możemy wybrać  i
i 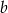 . Wypiszmy możliwe wybory dla
. Wypiszmy możliwe wybory dla  i
i 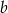 .
.
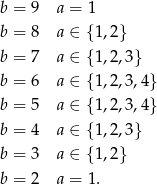
Jest więc
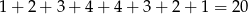
zdarzeń sprzyjających i prawdopodobieństwo jest równe
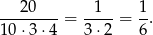
Odpowiedź: