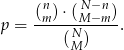Zadanie nr 9479341
W urnie znajduje się  losów, przy czym
losów, przy czym  z nich to losy wygrywające (
z nich to losy wygrywające ( ). Wybieramy losowo
). Wybieramy losowo  losów z urny (
losów z urny (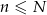 ) i niech
) i niech 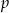 oznacza prawdopodobieństwo, że dokładnie
oznacza prawdopodobieństwo, że dokładnie 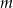 spośród tych losów to losy wygrywające (
spośród tych losów to losy wygrywające (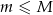 oraz
oraz 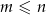 ). Uzasadnij, że
). Uzasadnij, że
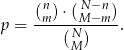
Rozwiązanie
Sposób I
Skoro losujemy  spośród
spośród 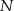 losów to
losów to
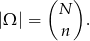
Policzmy teraz ile jest zdarzeń sprzyjających.
Mamy mieć 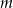 losów wygrywających – możemy je wybrać na
losów wygrywających – możemy je wybrać na
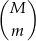
sposobów. Pozostałe 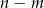 losów musimy wybrać spośród losów przegrywających, co możemy zrobić na
losów musimy wybrać spośród losów przegrywających, co możemy zrobić na
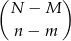
sposobów. W sumie jest więc
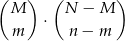
zdarzeń sprzyjających i prawdopodobieństwo wynosi
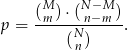
No i fajnie, ale nie wygląda to jak wynik, który mieliśmy uzyskać. Żeby zobaczyć, że to jednak jest to samo, obliczmy oba ilorazy.
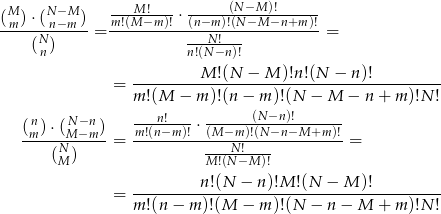
Widać teraz, że rzeczywiście jest to sama liczba napisana na dwa różne sposoby.
Sposób II
Tym razem policzymy prawdopodobieństwo w trochę nietypowy sposób, dzięki czemu od razu otrzymamy wynik w postaci z treści zadania.
Zamiast myśleć o losowaniu  losów z urny, możemy myśleć inaczej: ustalamy
losów z urny, możemy myśleć inaczej: ustalamy  spośród
spośród 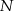 losów, a potem losujemy, które
losów, a potem losujemy, które 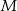 spośród wszystkich
spośród wszystkich 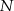 losów będą wygrywające. Przy takim podejściu mamy
losów będą wygrywające. Przy takim podejściu mamy
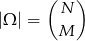
(wybieramy, które losy są wygrywające).
Policzmy teraz zdarzenia sprzyjające, tzn. takie zdarzenia, że dokładnie 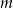 spośród naszych ustalonych
spośród naszych ustalonych  losów jest wygrywających. Te
losów jest wygrywających. Te 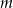 losów wygrywających możemy wybrać na
losów wygrywających możemy wybrać na
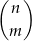
sposobów. Ponadto musimy wciąż ustalić, które 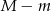 spośród losów spoza naszego ustalonego zbioru będą wygrywające. Możemy to zrobić na
spośród losów spoza naszego ustalonego zbioru będą wygrywające. Możemy to zrobić na
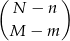
sposobów.
Prawdopodobieństwo jest więc równe