Zadanie nr 9810316
W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe 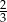 ?
?
Rozwiązanie
W sumie losujemy dwie kule z urny, więc jeżeli oznaczymy przez  szukaną liczbę białych kul, to mamy
szukaną liczbę białych kul, to mamy
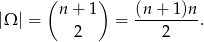
Dwie kule białe można wylosować na
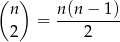
sposobów. Mamy więc równanie
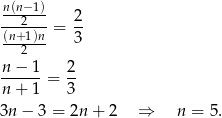
Odpowiedź: 5 kul

