/Szkoła średnia/Zadania maturalne/Matura 2019/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 30 marca 2019 Czas pracy: 180 minut
Zadania zamknięte
Dane są liczby 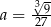 ,
, 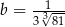 ,
, 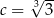 ,
, 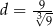 oraz
oraz 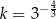 . Prawdziwa jest równość
. Prawdziwa jest równość
A) 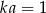 B)
B) 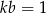 C)
C) 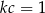 D)
D) 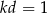
Okrąg o równaniu 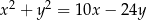 jest styczny do prostej
jest styczny do prostej
A) 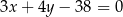 B)
B) 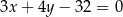 C)
C) 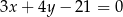 D)
D) 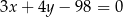
Ile jest liczb  należących do przedziału
należących do przedziału 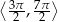 , które spełniają równanie
, które spełniają równanie 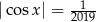 ?
?
A) 2 B) 8 C) 6 D) 4
Niech 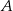 i
i 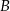 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 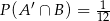 i
i 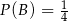 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 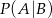 jest równe
jest równe
A) 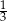 B)
B)  C)
C)  D)
D) 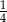
Granica ciągu 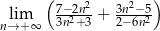 jest równa
jest równa
A) 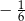 B)
B)  C)
C) 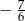 D)
D) 
Zadania otwarte
Wykres funkcji 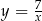 przesunięto o wektor
przesunięto o wektor ![→ v = [− 3,k]](https://img.zadania.info/zes/0059791/HzesT32x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 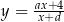 . Wyznacz
. Wyznacz 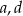 i
i 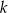 .
.
Reszta z dzielenia wielomianu 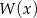 przez
przez 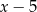 jest równa 4. Oblicz resztę z dzielenia wielomianu
jest równa 4. Oblicz resztę z dzielenia wielomianu 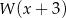 przez wielomian
przez wielomian 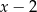 .
.
Oblicz sumę szeregu
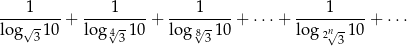
Wykaż, że równanie 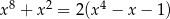 ma tylko jedno rozwiązanie rzeczywiste
ma tylko jedno rozwiązanie rzeczywiste 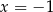 .
.
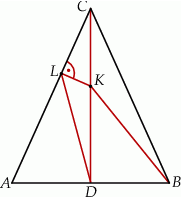
Odcinek 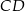 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 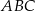 , w którym
, w którym 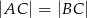 . Punkt
. Punkt 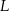 jest rzutem punktu
jest rzutem punktu 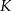 wysokości
wysokości 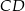 na bok
na bok 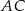 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 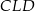 jest podobny do trójkąta
jest podobny do trójkąta 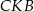 .
.
W trójkącie ostrokątnym 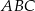 prawdziwa jest równość
prawdziwa jest równość 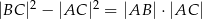 . Wykaż, że kąt
. Wykaż, że kąt 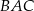 jest dwa razy większy od kąta
jest dwa razy większy od kąta 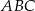 .
.
Grupę siedmiu osób, w których są trzy dziewczynki i czterech chłopców ustawiamy w rzędzie jeden za drugim. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie dziewczynki nie stoją bezpośrednio za sobą.
Oblicz sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 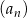 określonego dla
określonego dla 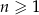 , w którym
, w którym
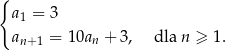
Wykaż, że jeżeli  i
i 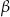 są kątami ostrymi, dla których
są kątami ostrymi, dla których 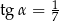 i
i 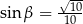 , to
, to 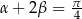 .
.
Wyznacz wszystkie wartości parametru 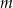 , dla których równanie
, dla których równanie
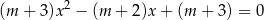
ma dwa różne rozwiązania 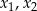 spełniające nierówność:
spełniające nierówność: 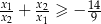 .
.
Funkcja 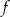 określona jest wzorem
określona jest wzorem 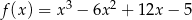 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 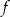 , które przechodzą przez punkt
, które przechodzą przez punkt 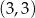 .
.
Rozpatrujemy wszystkie ostrosłupy prawidłowe czworokątne o krawędzi bocznej równej 3. Oblicz pole powierzchni całkowitej tego z tych ostrosłupów, dla którego pole przekroju płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy oraz wierzchołek ostrosłupa jest największe możliwe.

