/Szkoła średnia/Zadania maturalne/Matura 2019/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 13 kwietnia 2019 Czas pracy: 180 minut
Zadania zamknięte
Wartość wyrażenia 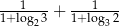 jest równa
jest równa
A) 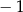 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Wektor 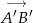 jest obrazem wektora
jest obrazem wektora 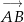 w jednokładności o środku
w jednokładności o środku 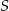 i skali
i skali 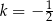 . Zatem
. Zatem
A) 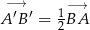 B)
B) 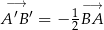 C)
C) 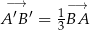 D)
D) 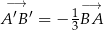
Największa wartość funkcji 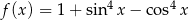 określonej dla
określonej dla 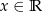 to
to
A) 1 B) 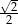 C)
C) 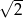 D) 2
D) 2
Spośród poniższych nierówności wskaż tę, którą spełniają wszystkie liczby całkowite.
A) 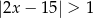 B)
B) 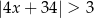 C)
C) 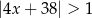 D)
D) 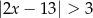
W rozwinięciu wyrażenia 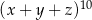 współczynnik przy iloczynie
współczynnik przy iloczynie 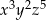 jest równy
jest równy
A) 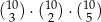 B)
B) 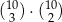 C)
C) 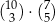 D)
D) 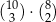
Zadania otwarte
Oblicz granicę jednostronną 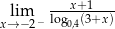 .
.
Oblicz sumę kwadratów pierwiastków równania 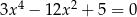 .
.
Wykaż, że
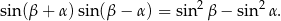
Na bokach 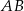 ,
, 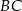 i
i 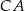 trójkąta
trójkąta 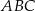 wybrano odpowiednio punkty
wybrano odpowiednio punkty 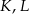 i
i 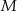 w ten sposób, że
w ten sposób, że 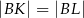 i
i 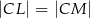 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 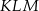 przecina bok
przecina bok 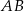 tego trójkąta w punkcie
tego trójkąta w punkcie 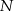 takim, że
takim, że 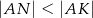 (zobacz rysunek).
(zobacz rysunek).
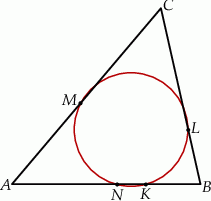
Udowodnij, że 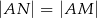 .
.
Dany jest nieskończony ciąg geometryczny 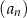 określony dla
określony dla 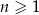 , którego wyrazy są niezerowe i iloraz
, którego wyrazy są niezerowe i iloraz 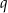 spełnia warunek:
spełnia warunek: 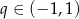 . Suma
. Suma 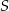 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 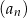 , suma
, suma 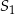 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 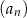 o numerach nieparzystych oraz suma
o numerach nieparzystych oraz suma 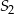 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 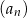 o numerach parzystych są kolejnymi wyrazami ciągu geometrycznego. Oblicz
o numerach parzystych są kolejnymi wyrazami ciągu geometrycznego. Oblicz 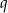 .
.
Na osi liczbowej każde dwie spośród 1000 kolejnych liczb naturalnych 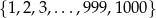 połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
Obwód równoległoboku 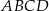 jest równy 26, miara jego kąta rozwartego
jest równy 26, miara jego kąta rozwartego 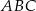 jest równa
jest równa 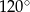 , a promień okręgu wpisanego w trójkąt
, a promień okręgu wpisanego w trójkąt 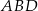 jest równy
jest równy 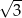 . Oblicz długości boków równoległoboku
. Oblicz długości boków równoległoboku 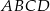 .
.
Prosta 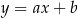 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 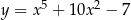 . Wykaż, że
. Wykaż, że 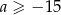 .
.
W sześcian o krawędzi 4 wpisano kulę styczną do trzech ścian sześcianu oraz przechodzącą przez środek sześcianu. Oblicz promień tej kuli.
W trójkącie 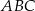 o polu 20 dane sa współrzędne dwóch wierzchołków:
o polu 20 dane sa współrzędne dwóch wierzchołków: 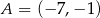 ,
, 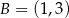 oraz środek
oraz środek 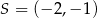 okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka
okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka 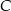 .
.
Wyznacz wszystkie wartości parametru 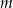 , dla których równanie
, dla których równanie 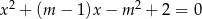 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 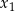 i
i 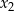
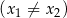 , spełniające warunek
, spełniające warunek 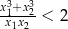 .
.
Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okrąg, i w których suma długości dłuższej podstawy i średnicy okręgu wpisanego jest równa 6. Wyznacz wymiary tego spośród tych trapezów, który ma najmniejszy obwód. Oblicz ten obwód.

