/Szkoła średnia/Zadania maturalne/Matura 2019/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 9 marca 2019 Czas pracy: 170 minut
Zadania zamknięte
Cena nart po obniżce o 23% jest mniejsza o 108 zł od ceny nart po obniżce o 17%. Ile kosztowałby te narty po obniżce ceny o 20%?
A) 1386 zł B) 1440 zł C) 1494 zł D) 1530 zł
Liczba 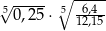 jest równa
jest równa
A)  B) 1,5 C)
B) 1,5 C) 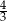 D)
D) 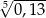
Wskaż nierówność, którą spełnia liczba 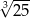 .
.
A) 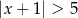 B)
B) 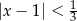 C)
C) 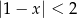 D)
D) 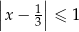
Liczba 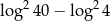 jest równa
jest równa
A) 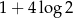 B)
B) 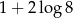 C)
C) 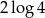 D)
D) 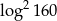
Na rysunku przedstawiony jest przedział 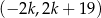 , gdzie
, gdzie 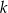 jest liczbą całkowitą. Suma wszystkich liczb całkowitych nieparzystych należących do tego przedziału jest równa 171.
jest liczbą całkowitą. Suma wszystkich liczb całkowitych nieparzystych należących do tego przedziału jest równa 171.
![]()
Stąd wynika, że
A) 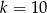 B)
B) 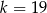 C)
C) 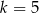 D)
D) 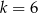
Liczby 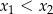 są rozwiązaniami równania
są rozwiązaniami równania 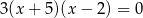 . Różnica
. Różnica 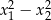 jest równa
jest równa
A) 21 B) 29 C) 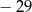 D)
D) 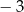
Średnia arytmetyczna zestawu danych: 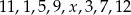 o medianie 6,5 jest równa
o medianie 6,5 jest równa
A) 8 B) 7,5 C) 7 D) 6,75
Liczba 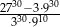 jest równa
jest równa
A) 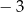 B)
B) 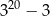 C)
C) 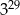 D)
D) 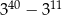
Wyrażenie 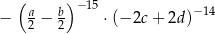 jest równe wyrażeniu
jest równe wyrażeniu
A) 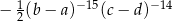 B)
B) 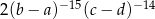
C) 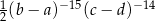 D)
D) 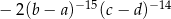
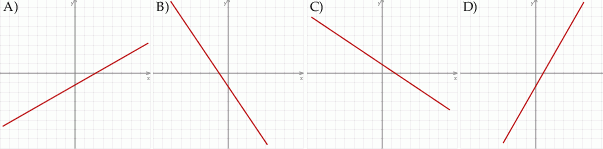
Na którym rysunku przedstawiono wykres funkcji liniowej 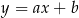 takiej, że
takiej, że 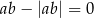 ?
?
Wykresem funkcji kwadratowej 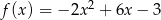 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 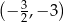 B)
B) 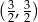 C)
C) 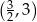 D)
D) 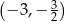
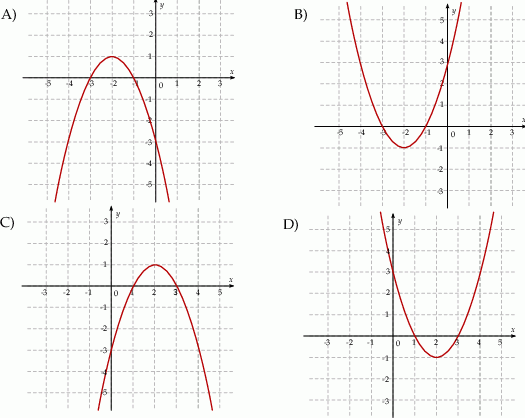
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem 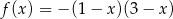 . Wskaż ten rysunek.
. Wskaż ten rysunek.
Na przyprostokątnych 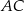 i
i 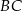 trójkąta prostokątnego
trójkąta prostokątnego 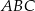 wybrano punkty
wybrano punkty 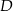 i
i 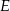 tak, że
tak, że 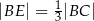 i
i 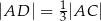 . Punkty
. Punkty 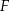 i
i 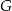 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 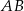 tak, że odcinki
tak, że odcinki 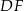 i
i 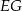 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 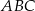 jest równe 36.
jest równe 36.
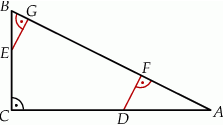
Zatem suma pól trójkątów 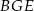 i
i 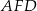 jest równa
jest równa
A) 4 B) 12 C) 18 D) 9
Rozwiązaniem równania 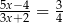 jest
jest
A) 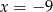 B)
B) 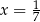 C)
C) 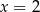 D)
D) 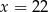
Przyprostokątna 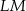 trójkąta prostokątnego
trójkąta prostokątnego 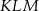 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 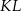 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
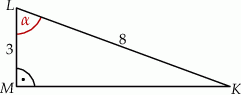
Wtedy miara  kąta ostrego
kąta ostrego 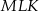 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 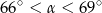 B)
B) 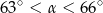 C)
C) 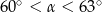 D)
D) 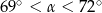
Dany jest ciąg arytmetyczny 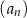 określony wzorem
określony wzorem 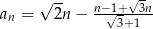 dla każdej liczby naturalnej
dla każdej liczby naturalnej 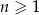 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 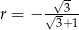 B)
B) 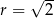 C)
C) 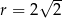 D)
D) 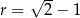
Dany jest ciąg geometryczny 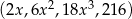 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 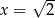 B)
B) 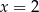 C)
C) 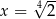 D)
D) 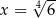
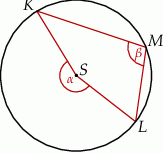
Dany jest okrąg o środku 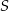 . Punkty
. Punkty 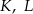 i
i 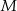 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 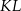 tego okręgu są oparte kąty
tego okręgu są oparte kąty 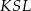 i
i 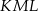 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 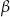 spełniają warunek
spełniają warunek 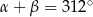 . Wynika stąd, że
. Wynika stąd, że
A) 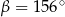 B)
B) 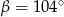 C)
C) 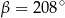 D)
D) 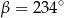
Punkt 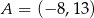 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 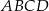 , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 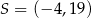 . Punkty
. Punkty 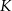 i
i 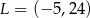 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków 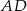 i
i 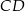 . Punkt
. Punkt 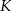 ma współrzędne
ma współrzędne
A) 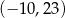 B)
B) 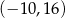 C)
C) 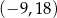 D)
D) 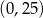
Kąt  jest rozwarty i
jest rozwarty i 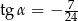 . Wobec tego
. Wobec tego
A) 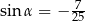 B)
B) 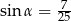 C)
C) 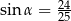 D)
D) 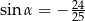
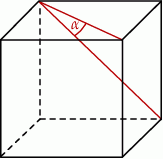
Jeżeli  oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
A) 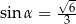 B)
B) 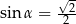 C)
C) 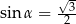 D)
D) 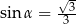
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa  i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
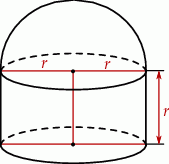
Pole powierzchni całkowitej tej bryły jest równe
A) 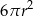 B)
B) 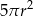 C)
C) 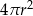 D)
D) 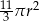
Łukasz dodał do siebie liczby krawędzi, wierzchołków oraz ścian pewnego graniastosłupa. Którą z liczb mógł otrzymać w wyniku?
A) 2018 B) 2019 C) 2020 D) 2021
Liczba wszystkich dodatnich liczb czterocyfrowych nieparzystych, w których zapisie nie występują cyfry 1 i 2, jest równa
A) 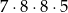 B)
B) 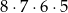 C)
C) 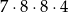 D)
D) 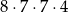
Pewnego dnia w klasie liczącej 16 dziewcząt i 12 chłopców nieobecnych było dwóch chłopców i trzy dziewczynki. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 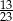 B)
B) 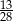 C)
C) 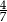 D)
D) 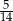
Zadania otwarte
Rozwiąż nierówność 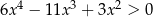 .
.
Wykaż, że jeżeli długości boków 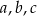 trójkąta prostokątnego są liczbami całkowitymi, to liczba
trójkąta prostokątnego są liczbami całkowitymi, to liczba 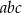 jest parzysta.
jest parzysta.
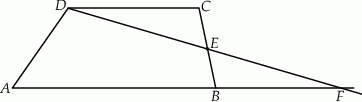
W trapezie 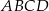 punkt
punkt 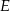 jest środkiem ramienia
jest środkiem ramienia 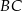 . Z wierzchołka
. Z wierzchołka 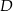 poprowadzono prostą przecinającą ramię
poprowadzono prostą przecinającą ramię 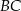 w punkcie
w punkcie 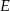 . Proste
. Proste 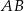 i
i 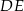 przecinają się w punkcie
przecinają się w punkcie 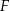 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 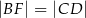 .
.
Liczby niezerowe 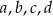 spełniają warunek
spełniają warunek 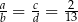 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 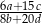 .
.
Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej  wzorem
wzorem 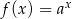 (gdzie
(gdzie 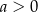 i
i 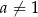 ), należy punkt
), należy punkt 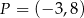 . Oblicz
. Oblicz  i zapisz zbiór wartości funkcji
i zapisz zbiór wartości funkcji 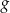 , określonej wzorem
, określonej wzorem 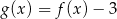 .
.
Ze zbioru 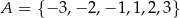 losujemy liczbę
losujemy liczbę  , natomiast ze zbioru
, natomiast ze zbioru 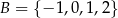 losujemy liczbę
losujemy liczbę 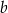 . Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej
. Te liczby są – odpowiednio – współczynnikiem kierunkowym i wyrazem wolnym funkcji liniowej 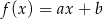 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymana funkcja 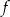 jest malejąca i ma dodatnie miejsce zerowe.
jest malejąca i ma dodatnie miejsce zerowe.
W ciągu arytmetycznym 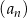 , określonym dla liczb naturalnych
, określonym dla liczb naturalnych 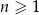 , wyraz piąty jest liczbą trzy razy mniejszą od wyrazu szóstego, a suma dwunastu początkowych wyrazów tego ciągu jest równa
, wyraz piąty jest liczbą trzy razy mniejszą od wyrazu szóstego, a suma dwunastu początkowych wyrazów tego ciągu jest równa 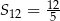 . Oblicz wyraz pierwszy oraz różnicę tego ciągu.
. Oblicz wyraz pierwszy oraz różnicę tego ciągu.
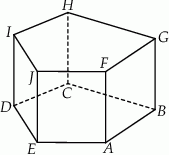
Dany jest graniastosłup prosty o podstawie pięciokątnej 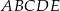 (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu dwa razy mniejszym niż pole pięciokąta 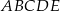 . Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.
. Pole powierzchni całkowitej tego graniastosłupa jest równe 153. Oblicz jego objętość.
Przekątne prostokąta 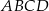 o obwodzie
o obwodzie 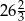 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 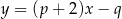 i
i 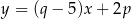 . Ponadto prosta
. Ponadto prosta 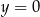 jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.
jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.

