/Szkoła średnia/Zadania maturalne/Matura 2019/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 16 marca 2019 Czas pracy: 180 minut
Zadania zamknięte
Liczba 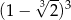 jest równa
jest równa
A) 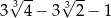 B)
B) 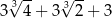 C)
C) 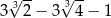 D)
D) 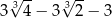
Punkt 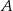 przesunięto o wektor
przesunięto o wektor ![[ ] − 123, 129](https://img.zadania.info/zes/0086505/HzesT6x.gif) i otrzymano punkt
i otrzymano punkt 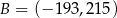 . Zatem
. Zatem
A) 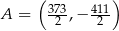 B)
B) 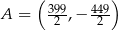 C)
C) 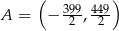 D)
D) 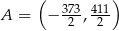
Wartość wyrażenia 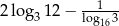 jest równa
jest równa
A) 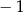 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Spośród poniższych nierówności wskaż tę, którą spełnia dokładnie sześć liczb całkowitych.
A) 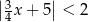 B)
B) 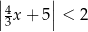 C)
C) 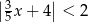 D)
D) 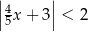
Na rysunku przedstawiono fragment wykresu funkcji 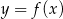
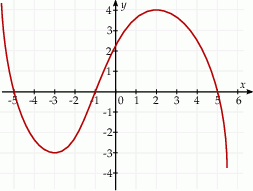
Pochodna 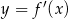 funkcji
funkcji 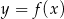 jest dodatnia w przedziale
jest dodatnia w przedziale
A) 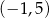 B)
B) 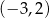 C)
C) 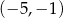 D)
D) 
Zadania otwarte
Oblicz granicę funkcji 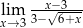 .
.
W pudełku znajduje się 6 kul czarnych i 4 kule białe. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 orły, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy jedną kulę. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.
Napisz równanie stycznych do wykresu funkcji 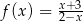 i równoległych do prostej o równaniu
i równoległych do prostej o równaniu 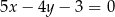 .
.
Czworokąt 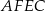 jest wpisany w okrąg i jego przekątna
jest wpisany w okrąg i jego przekątna 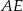 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 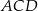 w punkcie
w punkcie 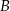 (zobacz rysunek).
(zobacz rysunek).
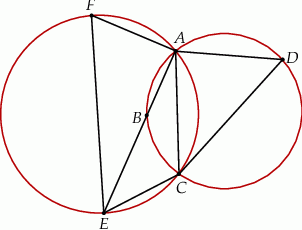
Zachodzi ponadto równość 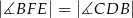 . Udowodnij, że punkty
. Udowodnij, że punkty 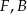 i
i 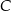 są współliniowe.
są współliniowe.
Rozwiąż nierówność 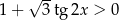 w przedziale
w przedziale 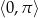 .
.
Trapez prostokątny 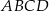 o podstawach
o podstawach 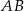 i
i 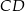 jest opisany na okręgu. Ramię
jest opisany na okręgu. Ramię 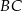 ma długość 15, a ramię
ma długość 15, a ramię 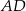 jest wysokością trapezu. Podstawa
jest wysokością trapezu. Podstawa 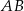 jest 3 razy dłuższa od podstawy
jest 3 razy dłuższa od podstawy 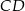 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Punkty 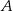 i
i 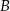 są punktami wspólnymi prostej o równaniu
są punktami wspólnymi prostej o równaniu 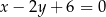 oraz okręgu o środku
oraz okręgu o środku 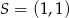 . Długość odcinka
. Długość odcinka 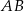 jest równa
jest równa 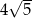 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 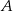 i
i 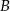 .
.
Cosinus kąta rozwarcia stożka jest równy 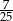 . Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
. Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
Sześcian największej z czterech różnych liczb całkowitych, tworzących rosnący ciąg arytmetyczny o wyrazach dodatnich, jest równy sumie sześcianów pozostałych liczb. Wykaż, że iloczyn dwóch z tych liczb jest o 60% większy od iloczynu dwóch pozostałych.
Wyznacz wszystkie wartości parametru 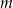 , dla których równanie
, dla których równanie 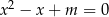 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 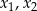 spełniające warunek
spełniające warunek 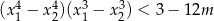 .
.
Rozważamy nieskończone ciągi geometryczne o ilorazie 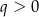 , w których kwadrat drugiego wyrazu jest dodatni i równy sumie wyrazów: drugiego, trzeciego i czwartego. Wyznacz pierwszy wyraz i iloraz tego spośród rozpatrywanych ciągów, którego suma wszystkich wyrazów jest najmniejsza. Oblicz tę sumę.
, w których kwadrat drugiego wyrazu jest dodatni i równy sumie wyrazów: drugiego, trzeciego i czwartego. Wyznacz pierwszy wyraz i iloraz tego spośród rozpatrywanych ciągów, którego suma wszystkich wyrazów jest najmniejsza. Oblicz tę sumę.

