/Gimnazjum/Egzamin gimnazjalny/Egzamin 2019/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 30 marca 2019 Czas pracy: 90 minut
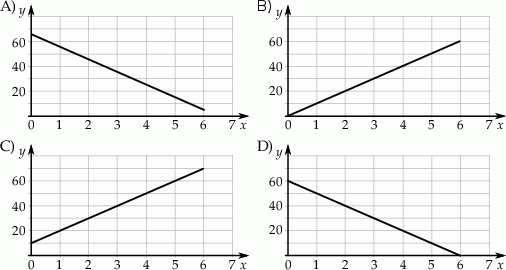
Na stacji paliw zatankowano do pełna 70 litrowy bak samochodu. Okazało się, że do baku wlano 60 litrów paliwa przy przepływie 10 litrów na minutę.
Który wykres przedstawia zależność ilości litrów paliwa w baku od czasu nalewania w minutach? Wybierz właściwą odpowiedź spośród podanych.
Na starym nagrobku rodzinnym wyryto datę śmierci ojca – MCMXIV oraz datę śmierci jego syna, który zmarł 27 lat później niż ojciec. Którą z dat wyryto na nagrobku jako datę śmierci syna? Wybierz właściwą odpowiedź spośród podanych.
A) MCMXLIII B) MCMXXXI C) MCMLI D) MCMXLI
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 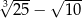 jest liczbą dodatnią. jest liczbą dodatnią. | P | F |
Liczba 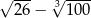 jest liczbą ujemną. jest liczbą ujemną. | P | F |
Samochód na pokonanie pierwszego odcinka trasy zużył 6,3 litra benzyny. Na drugim odcinku trasy, mającym długość 180 km, zużył on dwa razy więcej benzyny niż na pierwszym odcinku. Średnie zużycie benzyny na kilometr było na każdym odcinku trasy takie samo.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnie zużycie benzyny przez ten samochód na każde 100 km tej trasy było równe
A) 7 litrów. B) 3,5 litra. C) 14 litrów. D) 4,2 litra.
Zmieszano 2,5 szklanki octu 6% z 1,5 szklanki octu 10%. Jakie jest stężenie otrzymanej mieszanki? Wybierz odpowiedź spośród podanych.
A) 9% B) 8% C) 7% D) 7,5%
Dane są dwie liczby: 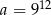 i
i 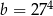 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn 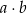 jest równy jest równy 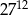 . . | P | F |
Iloraz 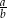 jest równy jest równy 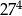 . . | P | F |
Ile razy liczba 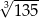 jest większa od liczby
jest większa od liczby 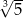 ?
?
Wybierz właściwą odpowiedź spośród podanych.
A) 27 B) 9 C) 6 D) 3
Grupa turystów w ciągu pierwszej godziny marszu pokonała pewien odcinek trasy. W każdej następnej godzinie pokonywany dystans był o 0,5 km dłuższy od dystansu pokonanego w poprzedniej godzinie. W ciągu pierwszych sześciu godzin marszu turyści przeszli łącznie 16,5 km trasy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odcinek trasy, który turyści przeszli w pierwszej godzinie marszu, miał długość
A) 4 km B) 2,5 km C) 3,5 km D) 1,5 km E) 2,1 km
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Wyrażenie 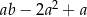 można przekształcić do postaci
można przekształcić do postaci
A) 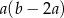 B)
B) 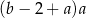 C)
C) 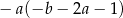 D)
D) 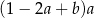
Dane są liczby  i
i 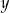 spełniające warunek:
spełniające warunek: 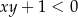 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby  i i 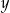 mają różne znaki. mają różne znaki. | P | F |
Suma liczb  i i 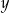 może być dodatnia. może być dodatnia. | P | F |
Długość modelu samolotu Albatros D.V wykonanego w skali 1:48 wynosi 153 mm.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe
Długość samolotu Albatros D.V wynosi około
A) 7,34 m B) 74 m C) 0,74 m D) 7,4 m
W pudełku są 2 kule zielone, 2 białe i 4 czarne. Losujemy z pudełka 1 kulę. Czy prawdziwe jest stwierdzenie, że prawdopodobieństwo wylosowania kuli czarnej jest dwa razy większe od prawdopodobieństwa wylosowania kuli białej? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w pudełku jest 2 razy mniej kul białych niż czarnych. |
| B) | w pudełku jest o połowę mniej kul zielonych niż kul czarnych. |
| C) | kule czarne stanowią połowę wszystkich kul w pudełku. |
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki równoległoboku.
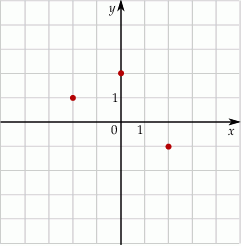
Który z punktów nie może być czwartym wierzchołkiem tego równoległoboku? Wybierz właściwą odpowiedź spośród podanych.
A) 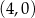 B)
B) 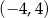 C)
C) 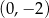 D)
D) 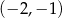
W układzie współrzędnych narysowano wykres funkcji i zaznaczono jego punkty przecięcia z prostą 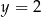 .
.
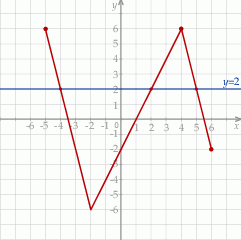
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość 2 dla pewnego argumentu będącego liczbą nieparzystą. | P | F |
Dla wszystkich argumentów większych od 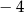 i jednocześnie mniejszych od 4 funkcja przyjmuje wartości mniejsze niż 2. i jednocześnie mniejszych od 4 funkcja przyjmuje wartości mniejsze niż 2. | P | F |
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
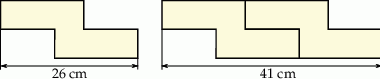
Ułożono wzór z 6 płytek, jak na rysunku.

Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Odcinek  ma długość
ma długość
A) 101 cm B) 156 cm C) 123 cm D) 90 cm
Dwa boki pewnego trójkąta mają długości 14 cm i 11 cm.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Trzeci bok tego trójkąta może mieć długość 24 cm. | P | F |
| Obwód tego trójkąta może być równy 29 cm. | P | F |
Trójkąt 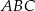 ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe
ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe 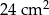 .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Najdłuższa wysokość trójkąta 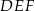 podobnego do trójkąta
podobnego do trójkąta 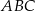 w skali 1:3 ma długość
w skali 1:3 ma długość
A) 4 cm B) 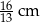 C) 2 cm D)
C) 2 cm D) 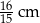
Na boku 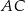 trójkąt równobocznego
trójkąt równobocznego 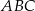 o polu równym
o polu równym 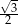 zbudowano równoramienny trójkąt prostokątny
zbudowano równoramienny trójkąt prostokątny 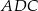 .
.
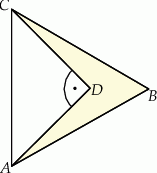
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole czworokąta 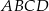 jest równe jest równe 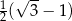 . . | P | F |
Obwód czworokąta 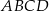 jest równy jest równy 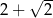 . . | P | F |
Kąt środkowy oparty na łuku okręgu długości 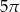 ma miarę
ma miarę 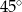 .
.
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Pole koła ograniczonego tym okręgiem jest równe
A) 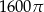 B)
B) 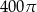 C)
C) 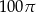 D)
D) 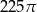
Półkole o promieniu 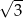 cm zwinięto w stożek.
cm zwinięto w stożek.
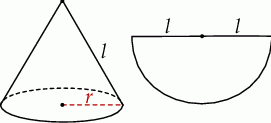
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Wysokość tego stożka jest równa
A) 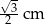 B)
B) 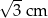 C) 3 cm D) 1,5 cm
C) 3 cm D) 1,5 cm
Punkty 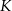 i
i 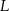 są środkami boków
są środkami boków 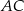 i
i 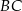 trójkąta
trójkąta 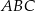 . Odcinki
. Odcinki 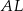 i
i 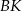 przecinają się w punkcie
przecinają się w punkcie 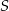 .
.
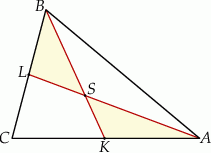
Uzasadnij, że pola trójkątów 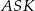 i
i 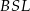 są równe.
są równe.
Schematyczny rysunek pokazuje położenie łódki na jeziorze.
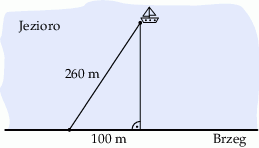
Jak jest odległość tej łódki od brzegu jeziora?
Organizator czterodniowego spływu kajakowego zapłacił za wypożyczenie kajaków 1696 zł. Na koszt wypożyczenia kajaków złożyła się stała dzienna opłata za usługę oraz dodatkowo koszt wypożyczenia każdego z kajaków.
| Opłata stała (niezależna od liczby kajaków) | 64 zł/dzień |
| Każdy z pierwszych 6 kajaków | 35 zł/dzień |
| Każdy kolejny kajak | 30 zł/dzień |
Ile osób wzięło udział w tym spływie, jeżeli w każdym kajaku płynęły dwie osoby?
Oskar zrobił dwa pudełka w kształcie graniastosłupów prawidłowych: czworokątnego i sześciokątnego. Powierzchnię boczną każdego z tych graniastosłupów wykonał z takich samych prostokątów o wymiarach 24 cm i 12 cm (patrz rysunek). Oblicz stosunek objętości tych graniastosłupów oraz ustal, który z nich ma większą objętość.


