/Szkoła średnia/Ciągi/Szereg geometryczny/Różne

Zadanie nr 3146288

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz iloraz nieskończonego, zbieżnego ciągu geometrycznego, w którym pierwszy wyraz jest równy 6, a suma wszystkich wyrazów tego ciągu stanowi 18 sumy ich kwadratów.

Rozwiązanie

Suma zbieżnego ciągu geometrycznego o ilorazie 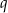q jest równa

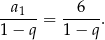
a1 6 ------= ------. 1− q 1 − q

Ciąg kwadratów wyrazów ciągu geometrycznego

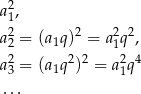
2 a1, a2 = (a1q )2 = a2q2, 22 22 12 4 a3 = (a1q ) = a1q ...

jest ciągiem geometrycznym o pierwszym wyrazie 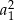2 a 1 i ilorazie 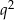2 q . Suma tego ciągu jest więc równa

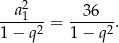
2 --a1---= --3-6--. 1− q2 1 − q 2

Pozostało rozwiązać równanie

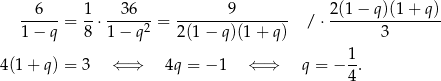
6 1 36 9 2(1 − q)(1 + q) ------= --⋅-----2-= ---------------- / ⋅---------------- 1 − q 8 1 − q 2(1 − q)(1 + q) 3 1- 4(1+ q) = 3 ⇐ ⇒ 4q = − 1 ⇐ ⇒ q = − 4.

 
Odpowiedź: q = − 14

Wersja PDF