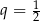/Szkoła średnia/Ciągi/Szereg geometryczny/Różne

Zadanie nr 4855061

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest nieskończony ciąg geometryczny 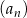(an) określony dla 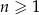n ≥ 1 , w którym 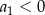a1 < 0 . Suma 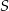S wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 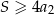S ≥ 4a2 . Wyznacz iloraz tego ciągu.

Rozwiązanie

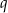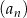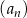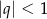Oznaczmy przez q iloraz ciągu (an) . Jeżeli istnieje suma wszystkich wyrazów ciągu (an) , to |q| < 1 . Wiemy ponadto, że

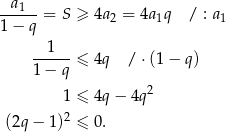
a1 ------= S ≥ 4a 2 = 4a1q / : a1 1 − q --1--- 1 − q ≤ 4q / ⋅(1 − q) 2 1 ≤ 4q − 4q 2 (2q − 1) ≤ 0.

Otrzymana nierówność oznacza, że 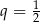1 q = 2 .  
Odpowiedź: q = 12

Wersja PDF