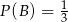/Szkoła średnia/Prawdopodobieństwo/Z definicji/Kostki

Zadanie nr 2711559

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucamy dwa razy symetryczną, sześcienną kostką do gry i zapisujemy sumę liczb wyrzuconych oczek.

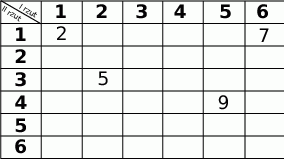
  • Uzupełnij tabelę, tak aby przedstawiała wszystkie możliwe wyniki tego doświadczenia.
  • Oblicz prawdopodobieństwo zdarzenia 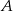A , polegającego na tym, że suma liczb oczek jest liczbą nieparzystą.
  • Oblicz prawdopodobieństwo zdarzenia 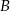B , polegającego na tym, że reszta z dzielenia sumy liczby oczek przez 3 jest równa 2.
PIC

Rozwiązanie

  • Uzupełniamy tabelkę.
    PIC
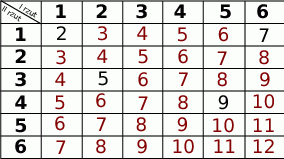
  • Za zdarzenia elementarlne przyjmijmy pary wyników rzutów (uwzględniamy porządek). Wszystkich takich par jest 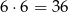6 ⋅6 = 36 zatem
    |Ω | = 3 6.

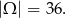
    Ilość zdarzeń sprzyjających do 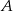A możemy odczytać z tabeli lub wyliczyć: jedna liczba musi być nieparzysta a druga parzysta, takich par jest (są dwa przypadki, pierwsza jest parzysta lub pierwsza jest nieparzysta)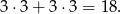

    3 ⋅3 + 3 ⋅3 = 18.

    Zatem

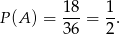
    P (A ) = 18-= 1. 36 2

     
    Odpowiedź: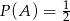 1 P(A ) = 2

  • Ilość zdarzeń sprzyjających najłatwiej odczytać z tabeli, odpowiadają im sumy oczek: 2, 5, 8 i 11 (tylko te liczby dają resztę 2 przy dzieleniu przez 3). W sumie jest ich 12.
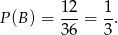
    12- 1- P (B) = 36 = 3.

     
    Odpowiedź: 1 P(B ) = 3

Wersja PDF