Zadanie nr 2929089
Rzucamy dziesięć razy sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych dziesięciu rzutach otrzymaliśmy dokładnie cztery razy sześć oczek, przy czym wyrzucono je w następującej konfiguracji
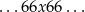
tzn. w pewnym momencie w dwóch kolejnych rzutach otrzymaliśmy szóstki, potem wyrzuciliśmy inną liczbę 
oczek, a następnie znowu wyrzuciliśmy dwie szóstki w dwóch kolejnych rzutach.
Rozwiązanie
W każdym rzucie mamy sześć możliwych wyników, więc jest
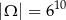
wszystkich możliwych zdarzeń. Zastanówmy się teraz ile jest zdarzeń sprzyjających – myślimy o nich jak o ciągach 10 wyników rzutu kostką. Jest 6 możliwości umieszczenia ciągu
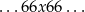
w 10 elementowym ciągu wyników (tzn. pierwsza szóstka może być na miejscach: 1,2,3,4,5,6). Potem możemy na 5 sposobów wybrać każdy z pozostałych wyników (nie może być szóstka). Jest więc
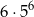
ciągów spełniających warunki zadania i interesujące nas prawdopodobieństwo jest równe
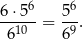
Odpowiedź: 
