Zadanie nr 5508881
Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w trzecim rzucie otrzymamy dwa razy więcej oczek niż w pierwszym rzucie.
Rozwiązanie
Sposób I
Przyjmijmy za zdarzenia elementarne uporządkowane trójki wylosowanych liczb. Zatem
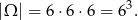
Zauważmy, że liczba oczek na trzeciej kostce jest jednoznacznie wyznaczona przez liczbę oczek na pierwszej kostce, a liczba oczek na drugiej kostce jest zupełnie dowolna. Ponadto liczba oczek na pierwszej kostce nie może być większa niż 3 (bo na trzeciej kostce nie może być 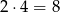 ). Zatem jest
). Zatem jest
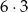
zdarzeń sprzyjających i prawdopodobieństwo wynosi
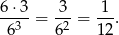
Sposób II
Zauważmy, że w ogóle nie interesuje nas wynik otrzymany na drugiej kostce, więc nie bierzmy jej pod uwagę. Mamy zatem
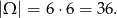
Na pierwszej kostce musi być jedna z liczb: 1,2,3. Na trzeciej kostce nie mamy żadnego wyboru, więc prawdopodobieństwo wynosi
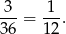
Odpowiedź: