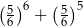/Szkoła średnia/Prawdopodobieństwo/Z definicji/Kostki

Zadanie nr 6638779

Rzucamy 6 razy symetryczną 6-ścienną kostką do gry. Oblicz prawdopodobieństwo

  • otrzymania co najmniej raz szóstki;
  • otrzymania co najwyżej raz szóstki.
Wersja PDF

Rozwiązanie

Jeżeli za zdarzenia elementarne przyjmiemy ciągi otrzymanych oczek, to mamy

|Ω | = 66.
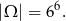
  • Łatwiej jest policzyć prawdopodobieństwo zdarzenia przeciwnego, czyli braku szóstki. Takich zdarzeń jest 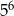6 5 (w każdym rzucie musi być jedna z liczb 1,2,3,4,5). Interesujące nas prawdopodobieństwo jest więc równe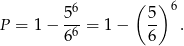
    ( ) 56- 5- 6 P = 1− 66 = 1 − 6 .

     
    Odpowiedź: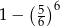 ( ) 1 − 56 6

  • Przed chwilą policzyliśmy, że jest 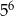6 5 zdarzeń bez szóstki. Policzmy ile jest zdarzeń z jedną szóstką. W którym rzucie wypadnie 6 możemy wybrać na 6 sposobów. Do tego w pozostałych rzutach jest dowolna z liczb 1,2,3,4,5, więc takich zdarzeń jest 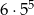6⋅55 i prawdopodobieństwo wynosi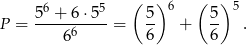
    6 5 ( ) 6 ( ) 5 P = 5-+-6-⋅5--= 5- + 5- . 66 6 6

     
    Odpowiedź: (5)6 (5)5 6 + 6

Wersja PDF