Zadanie nr 7008336
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 5.
Rozwiązanie
Zauważmy najpierw, że kwadrat liczby całkowitej przy dzieleniu przez 5 daje resztę 0, 1 lub 4. Rzeczywiście jeżeli 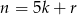 to
to
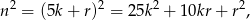
więc liczba 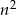 daje przy dzieleniu przez 5 taką samą resztę jak
daje przy dzieleniu przez 5 taką samą resztę jak 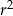 . Zatem dla
. Zatem dla 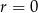 otrzymujemy resztę 0, dla
otrzymujemy resztę 0, dla 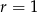 i
i 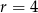 resztę 1, a dla
resztę 1, a dla 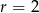 i
i 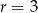 resztę 4.
resztę 4.
W przypadku liczby oczek na kostce mogliśmy to sprawdzić nawet prościej – wystarczy podnieść do kwadratu liczby od 1 do 6 i sprawdzić jakie otrzymujemy reszty.
Zastanówmy się teraz, kiedy suma trzech kwadratów może być podzielna przez 5. Patrząc na reszty (nie uwzględniamy na razie kolejności) są dwie możliwości
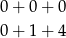
(tzn. albo wszystkie trzy liczby dzielą się przez 5, albo jedna dzieli się przez 5, kwadrat drugiej daje resztę 1, a kwadrat trzeciej resztę 4).
Teraz łatwo już obliczyć żądane prawdopodobieństwo. Za zdarzenia elementarne przyjmujemy ciągi otrzymanych oczek, czyli
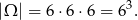
Jest jedno zdarzenie z trzema liczbami podzielnymi przez 5.
Obliczmy ile jest zdarzeń sprzyjających drugiego rodzaju. Liczbą podzielną przez 5 musi być 5. Liczbę, której kwadrat daje resztę 1 możemy wybrać ze zbioru 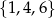 . Liczbę, której kwadrat ma dawać resztę 4 możemy wybrać ze zbioru
. Liczbę, której kwadrat ma dawać resztę 4 możemy wybrać ze zbioru 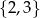 . Wybrane trzy liczby możemy ustawić w dowolnej kolejności, co w sumie daje
. Wybrane trzy liczby możemy ustawić w dowolnej kolejności, co w sumie daje
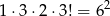
możliwości. Prawdopodobieństwo jest więc równe
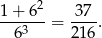
Odpowiedź: