Zadanie nr 7219862
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 3.
Rozwiązanie
Kluczowa jest w tym zadaniu obserwacja, że kwadrat liczby całkowitej  może dawać tylko resztę 1 lub 0 przy dzieleniu przez 3. Rzeczywiście, jeżeli
może dawać tylko resztę 1 lub 0 przy dzieleniu przez 3. Rzeczywiście, jeżeli 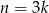 to liczba
to liczba 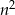 dzieli się przez 3, jeżeli
dzieli się przez 3, jeżeli 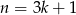 to
to
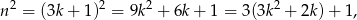
więc liczba ta daje resztę 1 z dzielenia przez 3. Podobnie, jeżeli 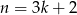 to
to
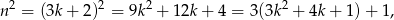
zatem znowu mamy liczbę, która przy dzieleniu przez 3 daje resztę 1.
Powyższa obserwacja oznacza, że suma kwadratów trzech liczb całkowitych dzieli się przez 3 (daje resztę 0) wtedy i tylko wtedy, gdy wszystkie 3 dzielą się przez 3 (czyli dają resztę 0), lub gdy wszystkie 3 nie dzielą się przez 3. Tak jest, bo jedyne sumy trzech 0 i 1-ek, które dają liczbę podzielną przez 3 to
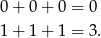
Możemy teraz policzyć prawdopodobieństwo. O zdarzeniach elementarnych myślimy jak o trójkach otrzymanych oczek, czyli
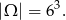
Zdarzenia sprzyjające to takie, że wszystkie trzy liczby dzielą się przez 3, czyli należą do zbioru 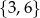 lub, że wszystkie 3 nie dzielą się przez 3, czyli należą do zbioru
lub, że wszystkie 3 nie dzielą się przez 3, czyli należą do zbioru 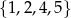 . Jest więc
. Jest więc
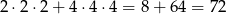
zdarzeń sprzyjających.
Prawdopodobieństwo wynosi
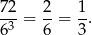
Odpowiedź: