Zadanie nr 7521911
Rzucamy trzykrotnie symetryczną kostką sześcienną do gry. Oblicz prawdopodobieństwa następujących zdarzeń:
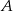 – na każdej kostce wypadnie nieparzysta liczba oczek,
– na każdej kostce wypadnie nieparzysta liczba oczek, 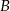 – suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 3.
– suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 3.
Rozwiązanie
Jak zwykle zaczynamy od wyboru odpowiedniej przestrzeni zdarzeń elementarnych. Ustalmy, że 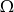 to wszystkie możliwe wyniki z uwzględnioną kolejnością, czyli np. odróżniamy
to wszystkie możliwe wyniki z uwzględnioną kolejnością, czyli np. odróżniamy 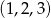 od
od 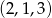 . W takim modelu wszystkich zdarzeń jest
. W takim modelu wszystkich zdarzeń jest 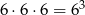 .
.
- Pierwsza część zadania jest łatwa, zdarzenia sprzyjające
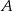 to takie, że wylosowane liczby są ze zbioru
to takie, że wylosowane liczby są ze zbioru 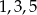 . Mamy zatem
. Mamy zatem 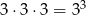 możliwości, skąd
możliwości, skąd 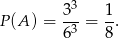
Odpowiedź: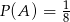
- Co do drugiego prawdopodobieństwa, to trzeba najpierw zrozumieć kiedy suma kwadratów trzech liczb dzieli się przez 3. Nie ma na to lepszego sposobu niż powypisywać sobie trochę możliwych wyników i poszukać jakiejś prawidłowości. My pominiemy ten krok i od razu podamy odpowiedź. Każda liczba przy dzieleniu przez trzy daje resztę
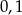 lub
lub 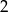 . Liczba jest podzielna przez 3, gdy reszta jest 0. Mamy zatem trzy liczby
. Liczba jest podzielna przez 3, gdy reszta jest 0. Mamy zatem trzy liczby 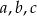 i zastanawiamy się kiedy
i zastanawiamy się kiedy 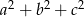 daje resztę 0 z dzielenia przez trzy. Sprawdźmy jaką resztę daje
daje resztę 0 z dzielenia przez trzy. Sprawdźmy jaką resztę daje 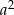 :
:
jeżeli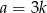 to reszta jest 0
to reszta jest 0
jeżeli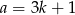 to
to 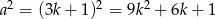 , czyli reszta jest 1
, czyli reszta jest 1
jeżeli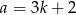 to
to 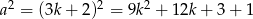 , czyli reszta jest 1
, czyli reszta jest 1
Widzimy zatem, że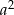 ma zawsze resztę 0 lub 1 z dzielenia przez 3. W końcu rozumiemy kiedy
ma zawsze resztę 0 lub 1 z dzielenia przez 3. W końcu rozumiemy kiedy 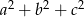 dzieli się przez trzy: albo
dzieli się przez trzy: albo 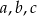 są wszystkie podzielne przez 3 (reszta 0+0+0) albo żadna z nich (reszta 1+1+1). Innych możliwości nie ma.
są wszystkie podzielne przez 3 (reszta 0+0+0) albo żadna z nich (reszta 1+1+1). Innych możliwości nie ma. Pozostało policzyć ile jest takich wyników. Układów z liczbami podzielnymi przez 3 jest
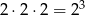 (bo do wyboru jest 3 i 6). Układów z liczbami, które nie są podzielne przez 3 jest
(bo do wyboru jest 3 i 6). Układów z liczbami, które nie są podzielne przez 3 jest 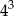 (do wyboru mamy 1,2,4 lub 5). Mamy zatem
(do wyboru mamy 1,2,4 lub 5). Mamy zatem 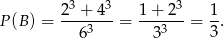
Odpowiedź: