Zadanie nr 7775474
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwo, że w każdym rzucie liczba oczek będzie większa od numeru rzutu.
Rozwiązanie
Za wyniki przyjmijmy trójki 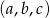 otrzymanych oczek. Zatem
otrzymanych oczek. Zatem
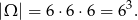
Zdarzenia sprzyjające możemy policzyć następująco: w pierwszym rzucie może wypaść jedna z 5 liczb (bo liczba oczek ma być większa od 1), w drugim jedna z 4 liczb (bo liczba oczek ma być większa od 2), a w trzecim jedna z 3 (bo liczba oczek ma być większa od 3). Wszystkich zdarzeń sprzyjających jest więc
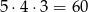
i prawdopodobieństwo wynosi
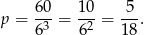
Odpowiedź: