Zadanie nr 8493303
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 4.
Rozwiązanie
Kluczowa jest w tym zadaniu obserwacja, że kwadrat liczby całkowitej  może dawać tylko resztę 1 lub 0 przy dzieleniu przez 4. Rzeczywiście, jeżeli
może dawać tylko resztę 1 lub 0 przy dzieleniu przez 4. Rzeczywiście, jeżeli  jest liczbą parzystą, tzn.
jest liczbą parzystą, tzn. 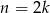 to liczba
to liczba 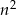 dzieli się przez 4, jeżeli natomiast
dzieli się przez 4, jeżeli natomiast  jest nieparzyste, tzn.
jest nieparzyste, tzn. 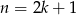 to
to
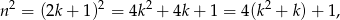
więc liczba ta daje resztę 1 z dzielenia przez 4.
Powyższa obserwacja oznacza, że suma kwadratów trzech liczb całkowitych dzieli się przez 4 (daje resztę 0) wtedy i tylko wtedy, gdy wszystkie 3 są parzyste (bo żadna z liczb 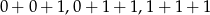 nie dzieli się przez 4).
nie dzieli się przez 4).
Możemy teraz obliczyć prawdopodobieństwo. O zdarzeniach elementarnych myślimy jak o trójkach otrzymanych oczek, czyli
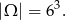
Zdarzenia sprzyjające to takie, że wszystkie trzy liczby są parzyste, czyli należą do zbioru 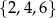 . Jest więc
. Jest więc
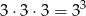
zdarzeń sprzyjających.
Prawdopodobieństwo wynosi
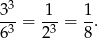
Odpowiedź: