/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2019/Egzamin
Egzamin Ósmoklasisty
z Matematyki 16 kwietnia 2019 Czas pracy: 100 minut
Na rysunku przedstawiono kartkę z kalendarza na rok 2017.

Natalia obchodzi urodziny 31 sierpnia, jej siostra Ewa – 18 sierpnia, a brat Karol – 2 października.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W 2017 r. urodziny Ewy wypadły w piątek. | P | F |
| W 2017 r. dniem urodzin Karola był poniedziałek. | P | F |
Liczba 1450 jest zaokrągleniem do rzędu dziesiątek kilku liczb naturalnych.
Ile jest wszystkich liczb naturalnych różnych od 1450, które mają takie zaokrąglenie? Wybierz właściwą odpowiedź spośród podanych.
A) 4 B) 5 C) 9 D) 10
W tabeli zapisano trzy wyrażenia.
| I | 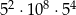 |
| II | 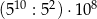 |
| III | 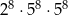 |
Które z tych wyrażeń są równe 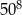 ?
?
Wybierz właściwą odpowiedź spośród podanych.
A) Tylko I i II. B) Tylko II i III. C) Tylko II. D) Tylko III.
Dane są cztery wyrażenia:
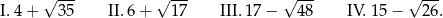
Wartości których wyrażeń są mniejsze od 10? Wybierz właściwą odpowiedź spośród podanych.
A) I i II B) II i III C) III i IV D) I, IV
Adam przygotował karty do gry z czterech arkuszy kartonu. Najpierw podzielił każdy arkusz kartonu na cztery części, a następnie każdą z nich ponownie podzielił na cztery części. Tak powstał komplet kart. W grze bierze udział 5 graczy, z których każdy otrzymuje jednakową liczbę kart.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Adam przygotował A/B karty do gry.
A) 32 B) 64
Każdy gracz może otrzymać maksymalnie C/D kart.
C) 12 D) 13
Dorota sporządziła z cukru i wody syrop do deseru. Stosunek masy cukru do masy wody w tym syropie jest równy 5 : 3.
Ile procent masy tego syropu stanowi masa cukru? Wybierz właściwą odpowiedź spośród podanych.
A) 25% B) 37,5% C) 40% D) 60% E) 62,5%
W pewnej firmie zatrudnionych jest więcej niż 10 pracowników. Połowa z nich zarabia po 3000 zł, a druga połowa – po 4000 zł.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia arytmetyczna zarobków w tej firmie jest równa 3500 zł. | P | F |
| Gdy z pracy w tej firmie zrezygnują dwie osoby, z których jedna zarabia 3000 zł, a druga 4000 zł, to średnia arytmetyczna zarobków się nie zmieni. | P | F |
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Wyrażenie 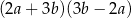 jest równe
jest równe
A) 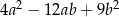 B)
B) 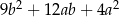 C)
C) 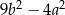 D)
D) 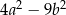
W układzie współrzędnych wyznaczono odcinek o końcach w punktach 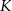 i
i 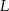 . Punkty te mają współrzędne
. Punkty te mają współrzędne 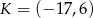 oraz
oraz 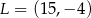 .
.
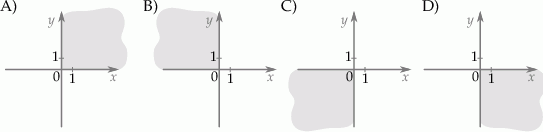
Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka 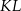 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
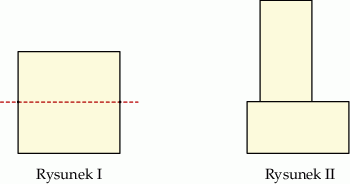
Kwadrat o boku  przedstawiony na rysunku I rozcięto na dwa przystające prostokąty, z których ułożono figurę, jak na rysunku II. Pole ułożonej figury jest równe polu kwadratu.
przedstawiony na rysunku I rozcięto na dwa przystające prostokąty, z których ułożono figurę, jak na rysunku II. Pole ułożonej figury jest równe polu kwadratu.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód ułożonej figury jest większy o 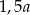 od obwodu kwadratu. od obwodu kwadratu. | P | F |
Obwód ułożonej figury jest równy 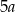 . . | P | F |
Na rysunku przedstawiono trzy trójkąty.
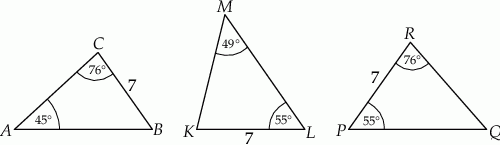
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Na podstawie informacji przedstawionych na rysunku można stwierdzić, że
A) trójkąt 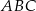 jest przystający do trójkąta
jest przystający do trójkąta 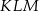 .
.
B) trójkąt 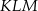 jest przystający do trójkąta
jest przystający do trójkąta 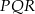 .
.
C) trójkąt 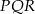 jest przystający do trójkąta
jest przystający do trójkąta 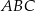 .
.
D) wszystkie trójkąty są do siebie przystające.
Na rysunku przedstawiono równoległobok 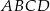 i trójkąt równoramienny
i trójkąt równoramienny 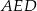 , w którym
, w którym 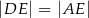 . Miara kąta
. Miara kąta 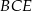 jest równa
jest równa 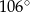 .
.
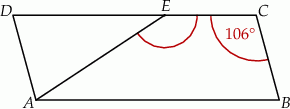
Jaką miarę ma kąt 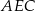 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) 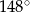 B)
B) 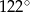 C)
C) 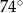 D)
D) 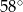
Na rysunku przedstawiono czworokąt zbudowany z dwóch trójkątów prostokątnych. Dane są długości boków 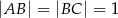 oraz
oraz 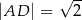 .
.
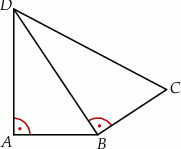
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość boku 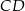 jest równa
jest równa
A) 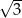 B) 2 C) 3 D)
B) 2 C) 3 D) 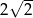
W koszu były 203 jednakowe sześcienne klocki. Zbudowano z nich możliwie największy sześcian, a pozostałe odłożono.
Ile klocków odłożono? Wybierz właściwą odpowiedź spośród podanych.
A) 150 B) 125 C) 78 D) 53
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.
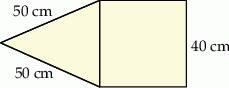
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Suma długości wszystkich krawędzi tego ostrosłupa jest równa
A) 560 cm B) 360 cm C) 260 cm D) 220 cm
Na diagramie przedstawiono informacje, jaki procent meczów w ciągu całego sezonu drużyna piłkarska zakończyła wygraną, jaki – przegraną, a jaki – remisem.
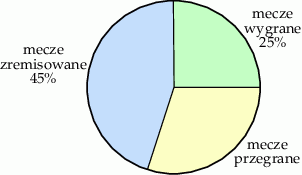
W ciągu całego sezonu drużyna wygrała 10 meczów. Ile meczów w sezonie ta drużyna przegrała?
Samochód osobowy przebył drogę 120 km w czasie 75 minut. Prędkość średnia busa na tej samej trasie wyniosła 80 km/h. O ile krótszy był czas przejazdu tej drogi samochodem osobowym od czasu przejazdu busem?
Adam zamówił bukiet złożony tylko z goździków i róż, w którym goździków było 2 razy więcej niż róż. Jedna róża kosztowała 4 zł, a cena jednego goździka wynosiła 3 zł. Czy wszystkie kwiaty w tym bukiecie mogły kosztować 35 zł?
Z okazji dnia sportu w godzinach od 9:00 do 12:00 przeprowadzono połowę z wszystkich konkurencji zaplanowanych na cały dzień, a między 12:00 a 14:00 – jeszcze 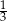 z pozostałych. O godzinie 14:00 z powodu deszczu zakończono zawody. W tym dniu nie przeprowadzono 12 zaplanowanych konkurencji. Ile konkurencji planowano przeprowadzić podczas całego dnia sportu?
z pozostałych. O godzinie 14:00 z powodu deszczu zakończono zawody. W tym dniu nie przeprowadzono 12 zaplanowanych konkurencji. Ile konkurencji planowano przeprowadzić podczas całego dnia sportu?
Prostokątną działkę o powierzchni 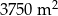 podzielono na trzy prostokątne działki o jednakowych wymiarach, w sposób przedstawiony na rysunku.
podzielono na trzy prostokątne działki o jednakowych wymiarach, w sposób przedstawiony na rysunku.

Jakie wymiary miała działka przed podziałem?
Paweł wyciął z kartonu trójkąt prostokątny 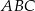 o przyprostokątnych 12 cm i 16 cm (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
o przyprostokątnych 12 cm i 16 cm (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt  wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez  (rysunek II).
(rysunek II).
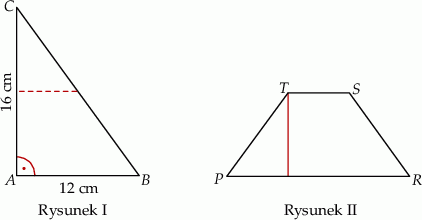
Oblicz różnicę obwodów trójkąta  i trapezu
i trapezu  .
.

