/Szkoła średnia/Zadania maturalne/Matura 2020
Egzamin Maturalny
z Matematyki (stara formuła)
poziom rozszerzony 15 czerwca 2020 Czas pracy: 180 minut
Rozwiąż nierówność 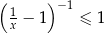 .
.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 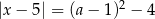 ma dwa różne rozwiązania dodatnie.
ma dwa różne rozwiązania dodatnie.
Liczby dodatnie  i
i 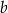 spełniają równość
spełniają równość 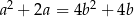 . Wykaż, że
. Wykaż, że 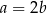 .
.
Dany jest trójkąt równoramienny 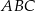 , w którym
, w którym 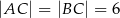 , a punkt
, a punkt 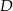 jest środkiem podstawy
jest środkiem podstawy 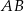 . Okrąg o środku
. Okrąg o środku 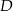 jest styczny do prostej
jest styczny do prostej 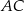 w punkcie
w punkcie 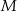 . Punkt
. Punkt 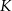 leży na boku
leży na boku 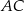 , punkt
, punkt 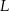 leży na boku
leży na boku 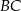 , odcinek
, odcinek 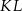 jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz 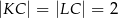 (zobacz rysunek).
(zobacz rysunek).
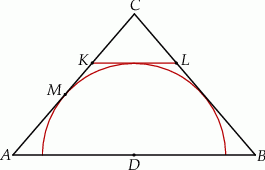
Wykaż, że 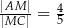 .
.
W trzywyrazowym ciągu geometrycznym 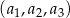 spełniona jest równość
spełniona jest równość 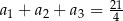 . Wyrazy
. Wyrazy 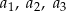 są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz
są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz 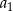 .
.
Rozwiąż równanie 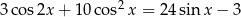 dla
dla 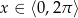 .
.
Dane jest równanie kwadratowe 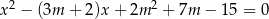 z niewiadomą
z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 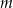 , dla których różne rozwiązania
, dla których różne rozwiązania 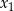 i
i 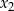 tego równania istnieją i spełniają warunek
tego równania istnieją i spełniają warunek
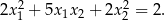
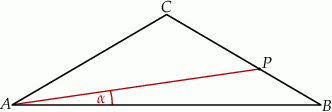
W trójkącie równoramiennym 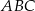 :
: 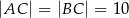 , a miara kąta
, a miara kąta 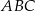 jest równa
jest równa 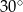 . Na boku
. Na boku 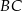 wybrano punkt
wybrano punkt 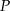 , taki, że
, taki, że 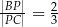 . Oblicz sinus kąta
. Oblicz sinus kąta  (zobacz rysunek).
(zobacz rysunek).
Prosta o równaniu 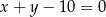 przecina okrąg o równaniu
przecina okrąg o równaniu 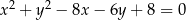 w punktach
w punktach 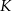 i
i 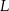 . Punkt
. Punkt 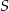 jest środkiem cięciwy
jest środkiem cięciwy 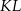 . Wyznacz równanie obrazu tego okręgu w jednokładności o środku
. Wyznacz równanie obrazu tego okręgu w jednokładności o środku 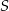 i skali
i skali 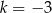 .
.
Dany jest kwadrat 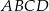 o boku długości 2. Na bokach
o boku długości 2. Na bokach 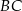 i
i 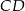 tego kwadratu wybrano – odpowiednio – punkty
tego kwadratu wybrano – odpowiednio – punkty 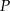 i
i 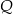 , takie, że długość odcinka
, takie, że długość odcinka 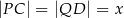 (zobacz rysunek). Wyznacz tę wartość
(zobacz rysunek). Wyznacz tę wartość  , dla której pole trójkąta
, dla której pole trójkąta 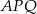 osiąga wartość najmniejszą. Oblicz to najmniejsze pole.
osiąga wartość najmniejszą. Oblicz to najmniejsze pole.
Oblicz, ile jest wszystkich siedmiocyfrowych liczb naturalnych, w których zapisie dziesiętnym występują dokładnie trzy cyfry 1 i dokładnie dwie cyfry 2.
Podstawą ostrosłupa czworokątnego 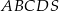 jest trapez
jest trapez 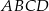 (
(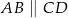 ). Ramiona tego trapezu mają długości
). Ramiona tego trapezu mają długości 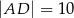 i
i 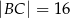 , a miara kąta
, a miara kąta 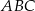 jest równa
jest równa 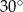 . Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt
. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt  , taki, że
, taki, że 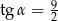 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

